Explorar el Código
Neue Aufgaben
Se han modificado 17 ficheros con 76 adiciones y 5 borrados
01_29_6MT22o_pr1_FCT3_4_Vecg/Lernziele.md → 01_22_6MT22o_pr1_FCT3_4_Vecg/Lernziele.md
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/Pruefung.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/Pruefung.tex
Ver fichero
|
||
| 28 | 28 |
|
| 29 | 29 |
|
| 30 | 30 |
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 31 |
|
|
| 32 |
|
|
| 33 |
|
|
| 34 |
|
|
| 35 |
|
|
| 34 | 36 |
|
| 35 | 37 |
|
| 36 | 38 |
|
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/PruefungHeader.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/PruefungHeader.tex
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/PruefungHeader_TRAINER.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/PruefungHeader_TRAINER.tex
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/clean.sh → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/clean.sh
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/dirMake.sh → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil1_OhneTR/dirMake.sh
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/Pruefung.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/Pruefung.tex
Ver fichero
|
||
| 24 | 24 |
|
| 25 | 25 |
|
| 26 | 26 |
|
| 27 |
|
|
| 28 |
|
|
| 27 |
|
|
| 28 |
|
|
| 29 | 29 |
|
| 30 | 30 |
|
| 31 | 31 |
|
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/PruefungHeader.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/PruefungHeader.tex
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/PruefungHeader_TRAINER.tex → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/PruefungHeader_TRAINER.tex
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/clean.sh → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/clean.sh
Ver fichero
01_29_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/dirMake.sh → 01_22_6MT22o_pr1_FCT3_4_Vecg/Teil2_mitTR/dirMake.sh
Ver fichero
+ 13
- 0
aufgaben/fct/log/BasiswechselIn10_v1.tex
Ver fichero
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
+ 20
- 0
aufgaben/fct/log/Dreiecksflaeche_v1.tex
Ver fichero
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 17 |
|
|
| 18 |
|
|
| 19 |
|
|
| 20 |
|
|
+ 13
- 0
aufgaben/fct/log/Log_Ablesen_v1.tex
Ver fichero
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
+ 13
- 0
aufgaben/fct/log/SchnittpunktMitUmkehrfunktion_v1.tex
Ver fichero
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
| 13 |
|
|
+ 10
- 0
aufgaben/fct/log/Umkehrfunktion_v1.tex
Ver fichero
|
||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
BIN
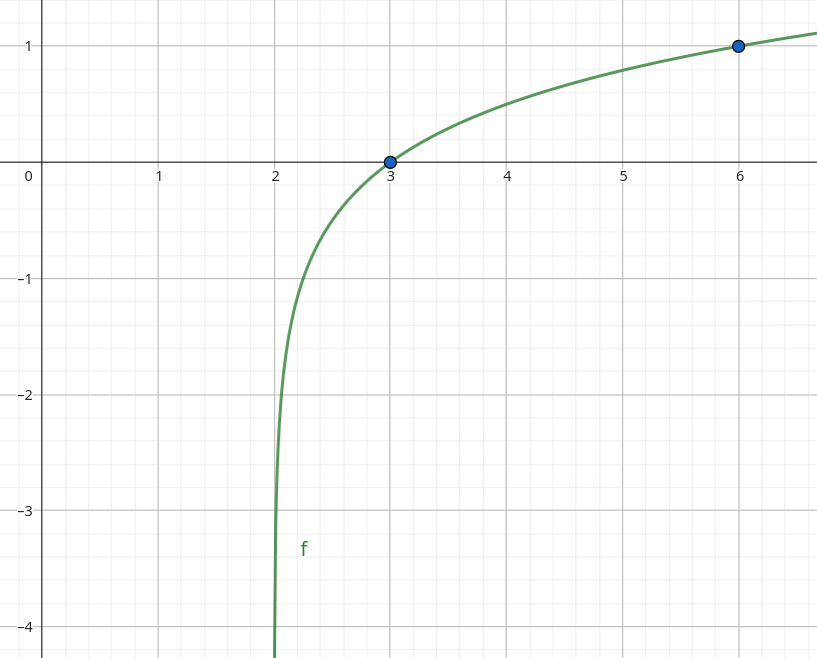
aufgaben/fct/log/img/Log_4_x-2_ablesen.png
Ver fichero
Loading…
