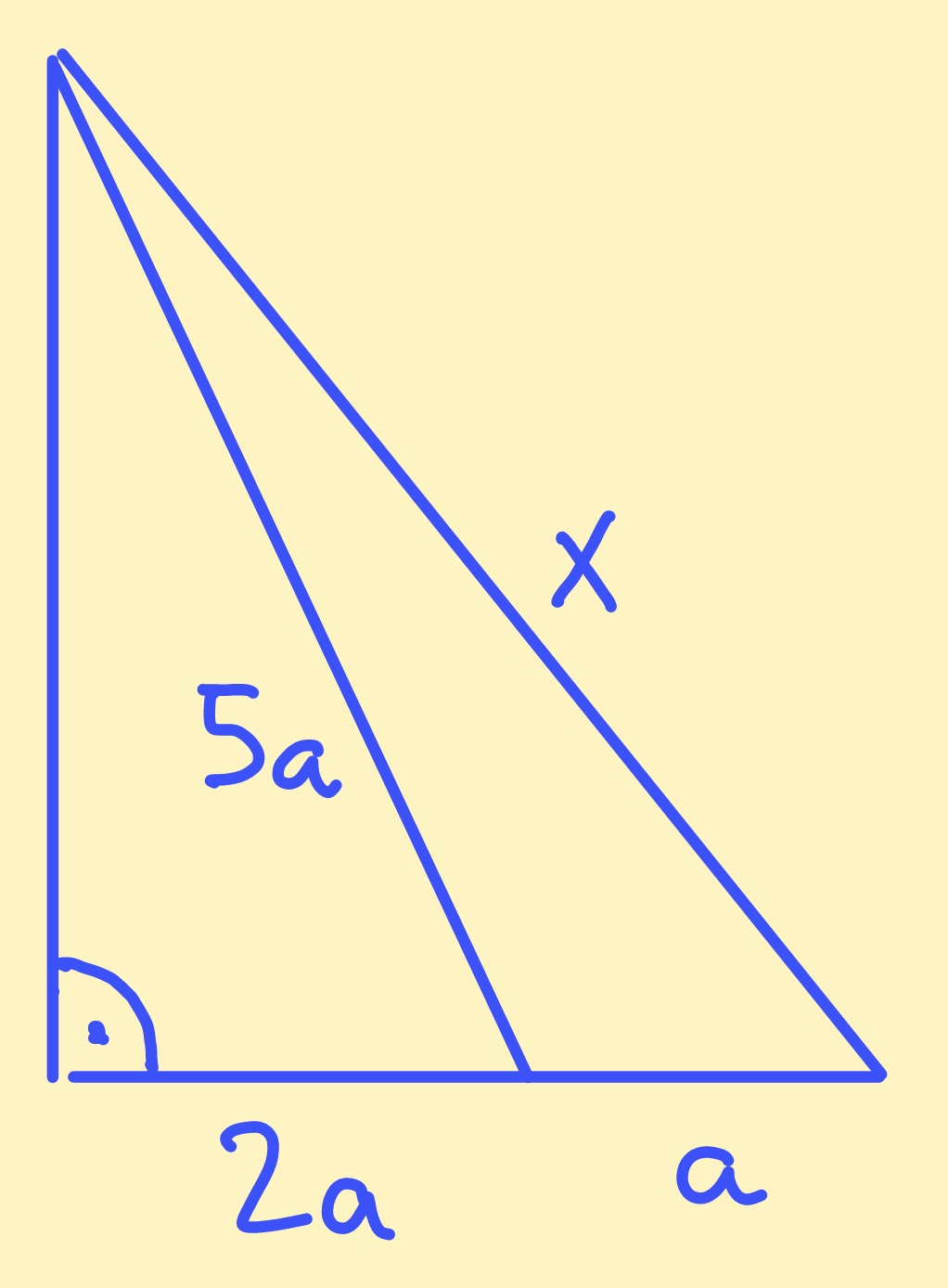
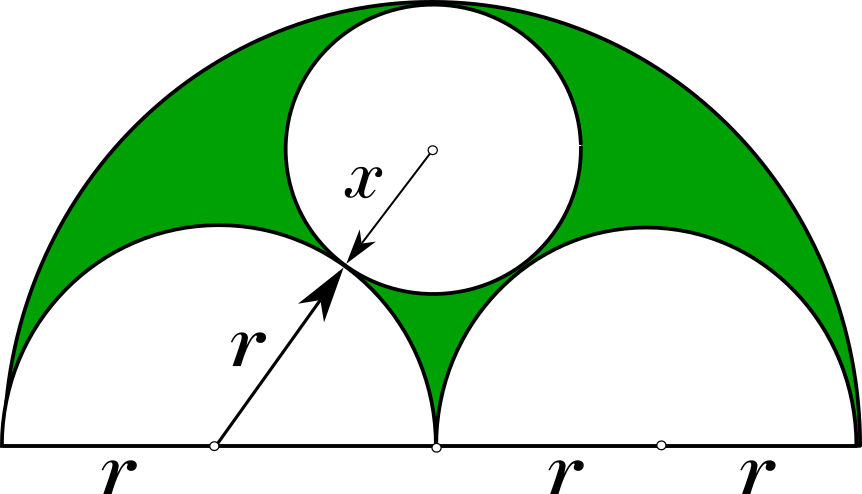
|
|
@@ -0,0 +1,304 @@
|
|
|
1
|
+<?xml version="1.0" encoding="UTF-8" standalone="no"?>
|
|
|
2
|
+<!-- Created with Inkscape (http://www.inkscape.org/) -->
|
|
|
3
|
+
|
|
|
4
|
+<svg
|
|
|
5
|
+ xmlns:dc="http://purl.org/dc/elements/1.1/"
|
|
|
6
|
+ xmlns:cc="http://creativecommons.org/ns#"
|
|
|
7
|
+ xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
|
|
|
8
|
+ xmlns:svg="http://www.w3.org/2000/svg"
|
|
|
9
|
+ xmlns="http://www.w3.org/2000/svg"
|
|
|
10
|
+ xmlns:sodipodi="http://sodipodi.sourceforge.net/DTD/sodipodi-0.dtd"
|
|
|
11
|
+ xmlns:inkscape="http://www.inkscape.org/namespaces/inkscape"
|
|
|
12
|
+ width="72.864021mm"
|
|
|
13
|
+ height="45.053715mm"
|
|
|
14
|
+ viewBox="0 0 72.864021 45.053715"
|
|
|
15
|
+ version="1.1"
|
|
|
16
|
+ id="svg8"
|
|
|
17
|
+ inkscape:version="0.92.4 (5da689c313, 2019-01-14)"
|
|
|
18
|
+ sodipodi:docname="vierKreise.svg"
|
|
|
19
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/arbelos.png"
|
|
|
20
|
+ inkscape:export-xdpi="90"
|
|
|
21
|
+ inkscape:export-ydpi="90">
|
|
|
22
|
+ <defs
|
|
|
23
|
+ id="defs2">
|
|
|
24
|
+ <marker
|
|
|
25
|
+ inkscape:stockid="Arrow1Lend"
|
|
|
26
|
+ orient="auto"
|
|
|
27
|
+ refY="0.0"
|
|
|
28
|
+ refX="0.0"
|
|
|
29
|
+ id="Arrow1Lend"
|
|
|
30
|
+ style="overflow:visible;"
|
|
|
31
|
+ inkscape:isstock="true">
|
|
|
32
|
+ <path
|
|
|
33
|
+ id="path887"
|
|
|
34
|
+ d="M 0.0,0.0 L 5.0,-5.0 L -12.5,0.0 L 5.0,5.0 L 0.0,0.0 z "
|
|
|
35
|
+ style="fill-rule:evenodd;stroke:#000000;stroke-width:1pt;stroke-opacity:1;fill:#000000;fill-opacity:1"
|
|
|
36
|
+ transform="scale(0.8) rotate(180) translate(12.5,0)" />
|
|
|
37
|
+ </marker>
|
|
|
38
|
+ <marker
|
|
|
39
|
+ inkscape:stockid="Arrow1Lend"
|
|
|
40
|
+ orient="auto"
|
|
|
41
|
+ refY="0"
|
|
|
42
|
+ refX="0"
|
|
|
43
|
+ id="Arrow1Lend-2"
|
|
|
44
|
+ style="overflow:visible"
|
|
|
45
|
+ inkscape:isstock="true">
|
|
|
46
|
+ <path
|
|
|
47
|
+ inkscape:connector-curvature="0"
|
|
|
48
|
+ id="path887-7"
|
|
|
49
|
+ d="M 0,0 5,-5 -12.5,0 5,5 Z"
|
|
|
50
|
+ style="fill:#000000;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:1.00000003pt;stroke-opacity:1"
|
|
|
51
|
+ transform="matrix(-0.8,0,0,-0.8,-10,0)" />
|
|
|
52
|
+ </marker>
|
|
|
53
|
+ </defs>
|
|
|
54
|
+ <sodipodi:namedview
|
|
|
55
|
+ id="base"
|
|
|
56
|
+ pagecolor="#ffffff"
|
|
|
57
|
+ bordercolor="#666666"
|
|
|
58
|
+ borderopacity="1.0"
|
|
|
59
|
+ inkscape:pageopacity="0.0"
|
|
|
60
|
+ inkscape:pageshadow="2"
|
|
|
61
|
+ inkscape:zoom="1.979899"
|
|
|
62
|
+ inkscape:cx="503.50185"
|
|
|
63
|
+ inkscape:cy="-190.02523"
|
|
|
64
|
+ inkscape:document-units="mm"
|
|
|
65
|
+ inkscape:current-layer="layer1"
|
|
|
66
|
+ showgrid="false"
|
|
|
67
|
+ inkscape:window-width="3792"
|
|
|
68
|
+ inkscape:window-height="2135"
|
|
|
69
|
+ inkscape:window-x="1920"
|
|
|
70
|
+ inkscape:window-y="0"
|
|
|
71
|
+ inkscape:window-maximized="1"
|
|
|
72
|
+ fit-margin-top="0"
|
|
|
73
|
+ fit-margin-left="0"
|
|
|
74
|
+ fit-margin-right="0"
|
|
|
75
|
+ fit-margin-bottom="0" />
|
|
|
76
|
+ <metadata
|
|
|
77
|
+ id="metadata5">
|
|
|
78
|
+ <rdf:RDF>
|
|
|
79
|
+ <cc:Work
|
|
|
80
|
+ rdf:about="">
|
|
|
81
|
+ <dc:format>image/svg+xml</dc:format>
|
|
|
82
|
+ <dc:type
|
|
|
83
|
+ rdf:resource="http://purl.org/dc/dcmitype/StillImage" />
|
|
|
84
|
+ <dc:title />
|
|
|
85
|
+ </cc:Work>
|
|
|
86
|
+ </rdf:RDF>
|
|
|
87
|
+ </metadata>
|
|
|
88
|
+ <g
|
|
|
89
|
+ inkscape:label="Layer 1"
|
|
|
90
|
+ inkscape:groupmode="layer"
|
|
|
91
|
+ id="layer1"
|
|
|
92
|
+ transform="translate(-73.03185,-61.870084)">
|
|
|
93
|
+ <path
|
|
|
94
|
+ style="opacity:1;vector-effect:none;fill:#00a105;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.3175;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
95
|
+ id="path815"
|
|
|
96
|
+ sodipodi:type="arc"
|
|
|
97
|
+ sodipodi:cx="109.73035"
|
|
|
98
|
+ sodipodi:cy="99.574203"
|
|
|
99
|
+ sodipodi:rx="36.215019"
|
|
|
100
|
+ sodipodi:ry="37.551369"
|
|
|
101
|
+ sodipodi:start="3.1415927"
|
|
|
102
|
+ sodipodi:end="0"
|
|
|
103
|
+ d="m 73.515327,99.574202 a 36.215019,37.551369 0 0 1 36.215023,-37.551367 36.215019,37.551369 0 0 1 36.21502,37.551368 l -36.21502,0 z"
|
|
|
104
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
105
|
+ inkscape:export-xdpi="300"
|
|
|
106
|
+ inkscape:export-ydpi="300" />
|
|
|
107
|
+ <path
|
|
|
108
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.32044661;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
109
|
+ id="path817"
|
|
|
110
|
+ sodipodi:type="arc"
|
|
|
111
|
+ sodipodi:cx="127.85045"
|
|
|
112
|
+ sodipodi:cy="99.589218"
|
|
|
113
|
+ sodipodi:rx="17.783356"
|
|
|
114
|
+ sodipodi:ry="18.479353"
|
|
|
115
|
+ sodipodi:start="3.1415927"
|
|
|
116
|
+ sodipodi:end="0"
|
|
|
117
|
+ d="M 110.06709,99.589217 A 17.783356,18.479353 0 0 1 127.85045,81.109865 17.783356,18.479353 0 0 1 145.6338,99.589218 H 127.85045 Z"
|
|
|
118
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
119
|
+ inkscape:export-xdpi="300"
|
|
|
120
|
+ inkscape:export-ydpi="300" />
|
|
|
121
|
+ <path
|
|
|
122
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.3175;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
123
|
+ id="path817-3"
|
|
|
124
|
+ sodipodi:type="arc"
|
|
|
125
|
+ sodipodi:cx="91.682846"
|
|
|
126
|
+ sodipodi:cy="99.587852"
|
|
|
127
|
+ sodipodi:rx="18.365007"
|
|
|
128
|
+ sodipodi:ry="18.679379"
|
|
|
129
|
+ sodipodi:start="3.1415927"
|
|
|
130
|
+ sodipodi:end="0"
|
|
|
131
|
+ d="M 73.317839,99.587852 A 18.365007,18.679379 0 0 1 91.682846,80.908474 18.365007,18.679379 0 0 1 110.04785,99.587852 H 91.682846 Z"
|
|
|
132
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
133
|
+ inkscape:export-xdpi="300"
|
|
|
134
|
+ inkscape:export-ydpi="300" />
|
|
|
135
|
+ <path
|
|
|
136
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.3175;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
137
|
+ id="path817-36"
|
|
|
138
|
+ sodipodi:type="arc"
|
|
|
139
|
+ sodipodi:cx="109.82512"
|
|
|
140
|
+ sodipodi:cy="74.495605"
|
|
|
141
|
+ sodipodi:rx="12.493567"
|
|
|
142
|
+ sodipodi:ry="12.239035"
|
|
|
143
|
+ sodipodi:start="6.2734452"
|
|
|
144
|
+ sodipodi:end="6.2396554"
|
|
|
145
|
+ d="M 122.31809,74.376398 A 12.493567,12.239035 0 0 1 110.05233,86.732616 12.493567,12.239035 0 0 1 97.335983,74.821554 12.493567,12.239035 0 0 1 109.3869,62.264102 12.493567,12.239035 0 0 1 122.30685,73.96301"
|
|
|
146
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
147
|
+ inkscape:export-xdpi="300"
|
|
|
148
|
+ inkscape:export-ydpi="300"
|
|
|
149
|
+ sodipodi:open="true" />
|
|
|
150
|
+ <text
|
|
|
151
|
+ xml:space="preserve"
|
|
|
152
|
+ style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:6.42342472px;line-height:1.25;font-family:Grey;-inkscape-font-specification:Grey;letter-spacing:0px;word-spacing:0px;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.19270274;stroke-miterlimit:4;stroke-dasharray:none"
|
|
|
153
|
+ x="98.773293"
|
|
|
154
|
+ y="81.386009"
|
|
|
155
|
+ id="text836"
|
|
|
156
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
157
|
+ inkscape:export-xdpi="300"
|
|
|
158
|
+ inkscape:export-ydpi="300"
|
|
|
159
|
+ transform="scale(1.0357246,0.96550763)"><tspan
|
|
|
160
|
+ sodipodi:role="line"
|
|
|
161
|
+ id="tspan834"
|
|
|
162
|
+ x="98.773293"
|
|
|
163
|
+ y="81.386009"
|
|
|
164
|
+ style="stroke-width:0.19270274;stroke-miterlimit:4;stroke-dasharray:none">x</tspan></text>
|
|
|
165
|
+ <text
|
|
|
166
|
+ xml:space="preserve"
|
|
|
167
|
+ style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:7.09527206px;line-height:1.25;font-family:Grey;-inkscape-font-specification:Grey;letter-spacing:0px;word-spacing:0px;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none"
|
|
|
168
|
+ x="87.026527"
|
|
|
169
|
+ y="98.729095"
|
|
|
170
|
+ id="text840-56"
|
|
|
171
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
172
|
+ inkscape:export-xdpi="300"
|
|
|
173
|
+ inkscape:export-ydpi="300"
|
|
|
174
|
+ transform="scale(1.0635503,0.940247)"><tspan
|
|
|
175
|
+ sodipodi:role="line"
|
|
|
176
|
+ id="tspan838-2"
|
|
|
177
|
+ x="87.026527"
|
|
|
178
|
+ y="98.729095"
|
|
|
179
|
+ style="stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none">r</tspan></text>
|
|
|
180
|
+ <path
|
|
|
181
|
+ style="fill:none;stroke:#000000;stroke-width:0.26675603px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1;marker-end:url(#Arrow1Lend)"
|
|
|
182
|
+ d="M 91.558823,99.40477 101.93605,84.913149"
|
|
|
183
|
+ id="path882"
|
|
|
184
|
+ inkscape:connector-curvature="0"
|
|
|
185
|
+ sodipodi:nodetypes="cc"
|
|
|
186
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
187
|
+ inkscape:export-xdpi="300"
|
|
|
188
|
+ inkscape:export-ydpi="300" />
|
|
|
189
|
+ <path
|
|
|
190
|
+ style="fill:none;stroke:#000000;stroke-width:0.16918093px;stroke-linecap:butt;stroke-linejoin:miter;stroke-opacity:1;marker-end:url(#Arrow1Lend-2)"
|
|
|
191
|
+ d="m 109.8264,74.487824 -7.16583,9.426882"
|
|
|
192
|
+ id="path882-0"
|
|
|
193
|
+ inkscape:connector-curvature="0"
|
|
|
194
|
+ sodipodi:nodetypes="cc"
|
|
|
195
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
196
|
+ inkscape:export-xdpi="300"
|
|
|
197
|
+ inkscape:export-ydpi="300" />
|
|
|
198
|
+ <path
|
|
|
199
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.10583333;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
200
|
+ id="path817-36-3"
|
|
|
201
|
+ sodipodi:type="arc"
|
|
|
202
|
+ sodipodi:cx="109.77822"
|
|
|
203
|
+ sodipodi:cy="74.571404"
|
|
|
204
|
+ sodipodi:rx="0.38691297"
|
|
|
205
|
+ sodipodi:ry="0.36865371"
|
|
|
206
|
+ sodipodi:start="6.2734452"
|
|
|
207
|
+ sodipodi:end="6.2396554"
|
|
|
208
|
+ d="m 110.16512,74.567813 a 0.38691297,0.36865371 0 0 1 -0.37986,0.372183 0.38691297,0.36865371 0 0 1 -0.39381,-0.358775 0.38691297,0.36865371 0 0 1 0.3732,-0.378244 0.38691297,0.36865371 0 0 1 0.40012,0.352384"
|
|
|
209
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
210
|
+ inkscape:export-xdpi="300"
|
|
|
211
|
+ inkscape:export-ydpi="300"
|
|
|
212
|
+ sodipodi:open="true" />
|
|
|
213
|
+ <text
|
|
|
214
|
+ xml:space="preserve"
|
|
|
215
|
+ style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:7.09527206px;line-height:1.25;font-family:Grey;-inkscape-font-specification:Grey;letter-spacing:0px;word-spacing:0px;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none"
|
|
|
216
|
+ x="127.56923"
|
|
|
217
|
+ y="110.2399"
|
|
|
218
|
+ id="text840-56-6"
|
|
|
219
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
220
|
+ inkscape:export-xdpi="300"
|
|
|
221
|
+ inkscape:export-ydpi="300"
|
|
|
222
|
+ transform="scale(1.0635503,0.94024701)"><tspan
|
|
|
223
|
+ sodipodi:role="line"
|
|
|
224
|
+ id="tspan838-2-0"
|
|
|
225
|
+ x="127.56923"
|
|
|
226
|
+ y="110.2399"
|
|
|
227
|
+ style="stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none">r</tspan></text>
|
|
|
228
|
+ <text
|
|
|
229
|
+ xml:space="preserve"
|
|
|
230
|
+ style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:7.09527206px;line-height:1.25;font-family:Grey;-inkscape-font-specification:Grey;letter-spacing:0px;word-spacing:0px;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none"
|
|
|
231
|
+ x="112.30277"
|
|
|
232
|
+ y="110.2399"
|
|
|
233
|
+ id="text840-56-62"
|
|
|
234
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
235
|
+ inkscape:export-xdpi="300"
|
|
|
236
|
+ inkscape:export-ydpi="300"
|
|
|
237
|
+ transform="scale(1.0635503,0.94024701)"><tspan
|
|
|
238
|
+ sodipodi:role="line"
|
|
|
239
|
+ id="tspan838-2-6"
|
|
|
240
|
+ x="112.30277"
|
|
|
241
|
+ y="110.2399"
|
|
|
242
|
+ style="stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none">r</tspan></text>
|
|
|
243
|
+ <text
|
|
|
244
|
+ xml:space="preserve"
|
|
|
245
|
+ style="font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;font-size:7.09527206px;line-height:1.25;font-family:Grey;-inkscape-font-specification:Grey;letter-spacing:0px;word-spacing:0px;fill:#000000;fill-opacity:1;stroke:none;stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none"
|
|
|
246
|
+ x="76.743919"
|
|
|
247
|
+ y="110.2399"
|
|
|
248
|
+ id="text840-56-1"
|
|
|
249
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
250
|
+ inkscape:export-xdpi="300"
|
|
|
251
|
+ inkscape:export-ydpi="300"
|
|
|
252
|
+ transform="scale(1.0635503,0.94024701)"><tspan
|
|
|
253
|
+ sodipodi:role="line"
|
|
|
254
|
+ id="tspan838-2-8"
|
|
|
255
|
+ x="76.743919"
|
|
|
256
|
+ y="110.2399"
|
|
|
257
|
+ style="stroke-width:0.21285817;stroke-miterlimit:4;stroke-dasharray:none">r</tspan></text>
|
|
|
258
|
+ <path
|
|
|
259
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.10583333;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
260
|
+ id="path817-36-3-7"
|
|
|
261
|
+ sodipodi:type="arc"
|
|
|
262
|
+ sodipodi:cx="91.296303"
|
|
|
263
|
+ sodipodi:cy="99.603897"
|
|
|
264
|
+ sodipodi:rx="0.38691297"
|
|
|
265
|
+ sodipodi:ry="0.36865371"
|
|
|
266
|
+ sodipodi:start="6.2734452"
|
|
|
267
|
+ sodipodi:end="6.2396554"
|
|
|
268
|
+ d="m 91.683197,99.600306 a 0.38691297,0.36865371 0 0 1 -0.379858,0.372184 0.38691297,0.36865371 0 0 1 -0.393812,-0.358775 0.38691297,0.36865371 0 0 1 0.373205,-0.378245 0.38691297,0.36865371 0 0 1 0.400117,0.352385"
|
|
|
269
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
270
|
+ inkscape:export-xdpi="300"
|
|
|
271
|
+ inkscape:export-ydpi="300"
|
|
|
272
|
+ sodipodi:open="true" />
|
|
|
273
|
+ <path
|
|
|
274
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.10583333;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
275
|
+ id="path817-36-3-9"
|
|
|
276
|
+ sodipodi:type="arc"
|
|
|
277
|
+ sodipodi:cx="110.10111"
|
|
|
278
|
+ sodipodi:cy="99.740929"
|
|
|
279
|
+ sodipodi:rx="0.38691297"
|
|
|
280
|
+ sodipodi:ry="0.36865371"
|
|
|
281
|
+ sodipodi:start="6.2734452"
|
|
|
282
|
+ sodipodi:end="6.2396554"
|
|
|
283
|
+ d="m 110.48801,99.737338 a 0.38691297,0.36865371 0 0 1 -0.37986,0.372182 0.38691297,0.36865371 0 0 1 -0.39381,-0.358773 0.38691297,0.36865371 0 0 1 0.3732,-0.378245 0.38691297,0.36865371 0 0 1 0.40012,0.352384"
|
|
|
284
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
285
|
+ inkscape:export-xdpi="300"
|
|
|
286
|
+ inkscape:export-ydpi="300"
|
|
|
287
|
+ sodipodi:open="true" />
|
|
|
288
|
+ <path
|
|
|
289
|
+ style="opacity:1;vector-effect:none;fill:#ffffff;fill-opacity:1;fill-rule:evenodd;stroke:#000000;stroke-width:0.10583333;stroke-linecap:square;stroke-linejoin:round;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1"
|
|
|
290
|
+ id="path817-36-3-2"
|
|
|
291
|
+ sodipodi:type="arc"
|
|
|
292
|
+ sodipodi:cx="129.12978"
|
|
|
293
|
+ sodipodi:cy="99.538101"
|
|
|
294
|
+ sodipodi:rx="0.38691297"
|
|
|
295
|
+ sodipodi:ry="0.36865371"
|
|
|
296
|
+ sodipodi:start="6.2734452"
|
|
|
297
|
+ sodipodi:end="6.2396554"
|
|
|
298
|
+ d="m 129.51667,99.534511 a 0.38691297,0.36865371 0 0 1 -0.37986,0.372183 0.38691297,0.36865371 0 0 1 -0.39381,-0.358775 0.38691297,0.36865371 0 0 1 0.3732,-0.378245 0.38691297,0.36865371 0 0 1 0.40012,0.352385"
|
|
|
299
|
+ inkscape:export-filename="/home/phi/matgit/pruefungen/aufgaben/P_ALLG/geometrie/planimetrie/img/vierkreise.png"
|
|
|
300
|
+ inkscape:export-xdpi="300"
|
|
|
301
|
+ inkscape:export-ydpi="300"
|
|
|
302
|
+ sodipodi:open="true" />
|
|
|
303
|
+ </g>
|
|
|
304
|
+</svg>
|