Prüfungsaufgaben und den Skript index angefügt

clean.sh

@@ -0,0 +1,11 @@
+if [ -f '../../layout/clean.sh' ] ; then
+  . ../../layout/clean.sh
+fi
+
+if [ -f '../../../layout/clean.sh' ] ; then
+  . ../../../layout/clean.sh
+fi
+
+if [ -f '../../../../layout/clean.sh' ] ; then
+  . ../../../../layout/clean.sh
+fi

makeBoth.sh

@@ -0,0 +1,29 @@
+
+#!/bin/bash
+#
+# CREATE two PDF from *.tex Files one: Trainer, one: Traniee
+#
+# author phi@freimann.eu
+# date   2019-07-11
+
+export ARTICLE_FILE_NAME="Pruefung"
+
+export ZIELGRUPPE="GESO"
+if [ -f './TALS.flag' ] ; then
+	export ZIELGRUPPE="TALS"
+fi
+
+
+export MAKE_DIR=$( cd "$( dirname "${BASH_SOURCE[0]}" )" >/dev/null 2>&1 && pwd )
+
+if [ -f '../../layout/makeBoth.sh' ] ; then
+		../../layout/makeBoth.sh
+fi
+
+if [ -f '../../../layout/makeBoth.sh' ] ; then
+		../../../layout/makeBoth.sh
+fi
+
+if [ -f '../../../../layout/makeBoth.sh' ] ; then
+		../../../../layout/makeBoth.sh
+fi

post_process.sh

@@ -0,0 +1,4 @@
+#!/bin/bash
+# 2019-07-04 ph. g. freimann bbw.ch
+#
+echo "Post Processing wäre hier"

pruefungsAufgaben/P_ALLG/KorrektesRunden_1Pkt.tex

@@ -0,0 +1,8 @@
+%%
+%% Zwei Punkte für korrektes Runden
+%%
+
+\begin{frage}[1]
+  Sie erhalten hiermit maximal zwei Punkte für korrektes Runden auf die angegebenen signifikanten Stellen (= signifikante Ziffern) in allen folgenden Aufgaben.
+  Bei ungelösten oder falsch gerundeten Aufgaben entfallen diese beiden Punkte ganz oder teilweise.
+\end{frage}

pruefungsAufgaben/P_ALLG/KorrektesRunden_2Pkt.tex

@@ -0,0 +1,9 @@
+%%
+%% Zwei Punkte für korrektes Runden
+%%
+
+\begin{frage}[2]
+  Sie erhalten hiermit maximal zwei Punkte für korrektes Runden auf die angegebenen signifikanten Stellen (= signifikante Ziffern) in \textbf{allen folgenden Aufgaben}.
+  Bei ungelösten oder falsch gerundeten Aufgaben entfallen diese beiden Punkte ganz oder teilweise.
+\end{frage}
+

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/gleichungfinden/FindeBasis_v1.tex

@@ -0,0 +1,8 @@
+\begin{frage}[2]
+  Die Exponentialfunktion $y=a^x$ gehe durch den Punkt
+  $P=(7|3.2)$. Finden Sie $a$ auf vier signifikante Ziffern:
+
+  $$a = \LoesungsRaum{1.181 \approx 1.1807672...}$$
+
+  \platzFuerBerechnungen{4.8}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/gleichungfinden/FindeCundA_v1.tex

@@ -0,0 +1,9 @@
+\begin{frage}[2]
+  Die Exponentialfunktion $y=ca^x$ gehe durch die Punkte $P=(1|6)$ und 
+  $Q=(-1 | 1.5)$. Finden Sie $a$ ($a$ > 0) und $c$:
+
+  $$a = \LoesungsRaum{2}$$
+  $$c = \LoesungsRaum{3}$$
+
+  \platzFuerBerechnungen{6.8}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/gleichungfinden/FindeCundA_v2.tex

@@ -0,0 +1,9 @@
+\begin{frage}[2]
+  Die Exponentialfunktion $y=ca^x$ gehe durch die Punkte $P=(1|12)$ und 
+  $Q=(-1 | \frac43)$. Finden Sie $a$ ($a$ > 0) und $c$:
+
+  $$a = \LoesungsRaum{3}$$
+  $$c = \LoesungsRaum{4}$$
+
+  \platzFuerBerechnungen{6.8}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/saettigung/BatterieLaden_v1.tex

@@ -0,0 +1,35 @@
+\begin{frage}[3]
+  Eine entladene (wiederaufladbare) 1.2 Volt-Batterie wird an eine Spannung von 1.3 Volt (Sättigung = 1.3)
+  angeschlossen, damit sich die Batterie wieder auflädt.
+
+  Am Anfang misst man eine Batteriespannung von 0.73
+  Volt (1. Messpunkt). Zwei Stunden später misst man
+  nochmals und die Batterie hat sich auf 0.96 Volt aufgeladen
+  (2. Messpunkt).
+  
+  Wie viel Zeit vergeht nach dem 1. Messpunkt, bis die Batterie auf
+  1.2 Volt aufgeladen ist?
+
+---
+  
+  Geben Sie die Funktionsgleichung an, welche die Batteriespannung in
+  Abhängigkeit von der Zeit (in Stunden) angibt.
+  Verwenden sie den 1. Messpunkt als Zeitpunt Null ($t_0=0$ und somit
+  $f(t_0) = f(0) = 0.73$).
+
+  $$f(t) = \LoesungsRaumLang{1.3 - 0.34 \cdot{} \left(\frac{0.34}{0.57} \right)^{frac{t}{2}}}$$
+
+  Wie viel Ladung hatte die Batterie nach einer Stunde (zwischen
+  1. und 2. Messpunkt)?
+
+  Nach einer Stunde (nach 1. Messpunkt) war die Batterie auf 
+  \LoesungsRaum{0.85977} Volt aufgeladen (mind. vier sign. Ziffern).
+
+\noTRAINER{  \vspace{1.5cm}}
+  
+  Die Batterie ist auf 1.2 Volt aufgeladen nach \LoesungsRaum{6.73697} Stunden nach dem
+  1. Messpunkt (mind. 4. sig. Ziffern).
+
+  (Eine Skizze kann hilfreich sein.)
+  \platzFuerBerechnungen{12.4}
+  \end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/wachstum/Stadtbevoelkerung_v1.tex

@@ -0,0 +1,14 @@
+\begin{frage}[2]
+Die Stadt Winterthur hatte in den letzten 50 Jahren ein durchschnittliches
+jährliches Bevölkerungswachstum von ca. 0.5\%.
+Im Jahre 2008 hat die Stadt zum ersten mal 100\,000 Einwohner
+überschritten.
+Angenommen es handle sich um ein exponentielles Wachstum:
+Wie viele Einwohner hatte Winterthur 1960?
+
+Winterthur hatte 1960 ca. \LoesungsRaumLang{79\,000} Einwohner (Geben Sie
+das Resultat auf 1000 Einwohner genau an, da es sowieso nicht genau
+stimmt.)
+
+\platzFuerBerechnungen{8.4}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/zinsfaktor/Abschreibung_Nach_n_Jahren_v1.tex

@@ -0,0 +1,11 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+  Das neue Mofa von Nadine kostete 2480.- CHF.
+
+  Jedes Jahr verliert das Mofa an 13\% Wert (Abschreibung).
+
+  Wie viel Wert hat das Mofa nach 9 Jahren noch?
+
+  Nach neun Jahren hat das Mofa noch einen Wert von CHF \LoesungsRaum{708.15}.
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/zinsfaktor/Abschreibung_Wert_v1.tex

@@ -0,0 +1,15 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+Ein neuer PC mit Bildschirm, Tastatur und Maus hatte einen Neupreis
+von CHF 3500.-.
+
+Heute nach mehreren Jahren und einer jährlichen Abschreibung von 23\% ist der Wert sichtlich auf unter CHF 1000.- gefallen.
+
+Nach wie vielen Jahren war dies frühestens geschehen?
+
+(Runden Sie auf das nächste ganze Jahr auf.)
+
+Nach \LoesungsRaum{5} Jahren ist der Wert frühestens unter CHF
+1\,000.- gefallen.
+
+  \platzFuerBerechnungen{10.4}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/zinsfaktor/Verzinsung_Wert_v1.tex

@@ -0,0 +1,18 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+A) Wie viele Jahre dauert es, bis sich ein Kapital von CHF 13860.- bei
+einer jährlichen Verzinsung von 10\% verdoppelt hat?
+
+(Runden Sie auf das nächste ganze Jahr auf.)
+Es dauert \LoesungsRaum{8} Jahre, bis sich das Vermögen von 13860.-
+CHF verdoppelt hat.
+
+\leserluft
+
+B) Wie lange dauert es, bis sich ein Kapital von 1\,000\,000.- bei der selben
+Verzinsung (10\%) verdoppelt hat? (Geben Sie eine Dezimalstelle; eine Stelle nach dem Komma an.)
+
+Es dauert \LoesungsRaum{7.27} Jahre, bis sich das Vermögen von 1\,000\,000.-
+CHF verdoppelt hat.
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/exponentialfct/zinsfaktor/Verzinsung_nach_n_Jahren_v1.tex

@@ -0,0 +1,19 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+Ein Kapital von CHF 10\,500.- wird mit einem Jahreszinssatz von 4.5\%
+verzinst.
+Auf wie viel ist das Kapital angewachsen...
+
+... nach einem Jahr: \LoesungsRaum{10\,972.50} CHF
+\leserluft
+(Lösungen auf 5 Rappen genau angeben!)
+
+\leserluft
+
+... nach zwei Jahren: \LoesungsRaum{11\,466.25} CHF 
+\leserluft
+
+... nach 25 Jahren: \LoesungsRaum{315\,570.06} CHF
+\leserluft
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Definitions_und_Wertebereich_v1.tex

@@ -0,0 +1,12 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+Geben Sie den Definitionsbereich $\mathbb{D}$ und den zugehörigen Wertebereich
+$\mathbb{W}$ der Funktion
+
+$$y=\frac{1}{x^5}$$
+an.
+
+$$\mathbb{D} = \LoesungsRaum{\mathbb{R}\backslash{}\{0\}}$$
+$$\mathbb{W} = \LoesungsRaum{\mathbb{R}\backslash{}\{0\}}$$
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}{

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Definitions_und_Wertebereich_v2.tex

@@ -0,0 +1,12 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+Geben Sie den Definitionsbereich $\mathbb{D}$ und den zugehörigen Wertebereich
+$\mathbb{W}$ der Funktion
+
+$$y=\frac{1}{x^4}$$
+an.
+
+$$\mathbb{D} = \LoesungsRaum{\mathbb{R}\backslash{}\{0\}}$$
+$$\mathbb{W} = \LoesungsRaum{\mathbb{R}^{+}}$$
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}{

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Finde_das_Uh_v1.tex

@@ -0,0 +1,9 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Finden Sie den Parameter $u$ der Funktion $y=\frac{1}{(x-u)^3}$,
+  wenn Sie wissen, dass die Funktion durch den Punkt $P = (3|\frac18)$ verläuft.
+  
+  $u=\LoesungsRaum{1}$
+  
+  \platzFuerBerechnungen{8}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/GemeinsamePunkte_v1.tex

@@ -0,0 +1,9 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+  Welche Punkte bzw. welchen Punkt haben die Funktionen $y=x^2$ und $y=x^{-1}$ gemeinsam?
+
+  \leserluft
+  
+  \LoesungsRaumLang{(1|1)}
+
+  \platzFuerBerechnungen{4.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/GemeinsamePunkte_v2.tex

@@ -0,0 +1,9 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+  Welche Punkte bzw. welchen Punkt haben die Funktionen $y=x^2$ und $y=x^{-2}$ gemeinsam?
+
+  \leserluft
+  
+  \LoesungsRaumLang{(1|1), (-1|1)}
+
+  \platzFuerBerechnungen{4.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/PotenzFunktionenZuordnen_v1.tex

@@ -0,0 +1,41 @@
+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+  Um Welche Potenzfunktionen $y= \pm x^n \pm v$ handelt es sich bei $A$, $B$, $C$, $D$, $E$ bzw. $F$?
+
+  Als Exponenten $n$ kommen die Zahlen $-2$, $2$, $3$ und $6$ vor. 
+
+
+  \leserluft
+  
+  \begin{tabular}{|c|c|c|}
+    \hline
+    $A$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p21_p0.png}&
+    $B$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_m_x_h_p21_p1.png}&
+    $C$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p61_p0.png}\\  \hline
+    $D$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p31_p1.png}&
+    $E$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_p0.png}&
+    $F$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_m2.png}\\ \hline
+    \end{tabular} 
+
+  \leserluft
+  \leserluft
+  
+  $A$: $y=\LoesungsRaum{x^2}$
+  \leserluft
+
+  $B$: $y=\LoesungsRaum{-x^2 + 1}$
+  \leserluft
+
+  $C$: $y=\LoesungsRaum{x^6}$
+  \leserluft
+  
+  $D$: $y=\LoesungsRaum{x^3 + 1}$
+  \leserluft
+  
+  $E$: $y=\LoesungsRaum{x^{-2}}$
+  \leserluft
+  
+  $F$: $y=\LoesungsRaum{x^{-2} - 2}$
+  
+  \platzFuerBerechnungen{6.4}
+  (Sie erhalten pro korrekte Funktion $\frac12$ Punkt.)
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/PotenzFunktionenZuordnen_v2.tex

@@ -0,0 +1,37 @@
+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+  Um Welche Potenzfunktionen $y= \pm x^n \pm v$ handelt es sich bei $A$, $B$, $C$, $D$, $E$ bzw. $F$?
+
+  \leserluft
+  
+  \begin{tabular}{|c|c|c|}
+    \hline
+    $A$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p21_p0.png}&
+    $B$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_p0.png}&
+    $C$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_m2.png}\\ \hline
+    $D$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_m_x_h_p21_p1.png}&
+    $E$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p61_p0.png}&
+    $F$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p31_p1.png}\\ \hline
+    \end{tabular} 
+
+  Die folgenden Funktionen kommen vor:
+  
+  \begin{tabular}{|c|c|c|}\hline
+    $f_1: y=x^2$ & $f_2: y= x^6$ & $f_3: y=x^3+1$\\\hline
+    $f_4: y=1-x^2$ & $f_5: y= x^{-2}$ & $f_6: y=x^{-2}-2$\\\hline
+    \end{tabular}
+
+  Ordnen Sie zu
+
+  \begin{tabular}{c|c}
+    Funktionsgraph & Funktionsnummer \\\hline
+    $A$ & \LoesungsRaum{$f_1$}\\\hline
+    $B$ & \LoesungsRaum{$f_5$}\\\hline
+    $C$ & \LoesungsRaum{$f_6$}\\\hline
+    $D$ & \LoesungsRaum{$f_4$}\\\hline
+    $E$ & \LoesungsRaum{$f_2$}\\\hline
+    $F$ & \LoesungsRaum{$f_3$}\\\hline
+    \end{tabular}
+  
+  \platzFuerBerechnungen{6.4}
+  (Sie erhalten pro korrekte Zuordnung 0.5 Pkt. Sie erhalten für eine falsche Zuordnung -1 Pkt.)
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/PotenzFunktionenZuordnen_v3.tex

@@ -0,0 +1,38 @@
+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+  Um Welche Potenzfunktionen $y= \pm x^n \pm v$ handelt es sich bei $A$, $B$, $C$, $D$, $E$ bzw. $F$?
+
+  \leserluft
+  
+  \begin{tabular}{|c|c|c|}
+    \hline
+    $A$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_m2.png}&
+    $B$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_m_x_h_p21_p1.png}&
+    $C$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p31_p1.png}\\ \hline
+    $D$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p21_p0.png}&
+    $E$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p61_p0.png}&
+    $F$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_p0.png}\\\hline
+    \end{tabular} 
+
+  \leserluft
+  Es kommen nur Funktionen aus der folgenden Aufzählung vor:
+  
+  \begin{tabular}{|c|c|c|c|}\hline
+    $f_1: y=x^2$   & $f_2: y=x^5-1$        & $f_3: y= x^6$    & $f_4: y=x^3+1$  \\\hline
+    $f_5: y=1-x^2$ & $f_6: y=-\frac{1}{x}$ & $f_7: y= x^{-2}$ & $f_8: y=x^{-2}-2$\\\hline
+    \end{tabular}
+
+  Ordnen Sie zu
+
+  \begin{tabular}{c|c}
+    Funktionsgraph & Funktionsnummer \\\hline
+    $A$ & \LoesungsRaum{$8$}\\\hline
+    $B$ & \LoesungsRaum{$5$}\\\hline
+    $C$ & \LoesungsRaum{$4$}\\\hline
+    $D$ & \LoesungsRaum{$1$}\\\hline
+    $E$ & \LoesungsRaum{$3$}\\\hline
+    $F$ & \LoesungsRaum{$7$}\\\hline
+    \end{tabular}
+  
+  \platzFuerBerechnungen{6.4}
+  (Sie erhalten pro korrekte Zuordnung 0.5 Pkt. Sie erhalten für eine falsche Zuordnung -0.5 Pkt.)
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/PotenzFunktionenZuordnen_v4.tex

@@ -0,0 +1,38 @@
+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+  Um Welche Potenzfunktionen $y= \pm x^n \pm v$ handelt es sich bei $A$, $B$, $C$, $D$, $E$ bzw. $F$?
+
+  \leserluft
+  
+  \begin{tabular}{|c|c|c|}
+    \hline
+    $A$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_m2.png}&
+    $B$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_m21_p0.png}&
+    $C$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_m_x_h_p21_p1.png}\\\hline
+    $D$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p31_p1.png}&
+    $E$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p21_p0.png}&
+    $F$ \includegraphics[width=4.5cm]{P_ALLG/funktionen/potenzfct/img/pot_p_x_h_p61_p0.png}\\\hline
+    \end{tabular} 
+
+  \leserluft
+  Es kommen nur Funktionen aus der folgenden Aufzählung vor:
+  
+  \begin{tabular}{|c|c|c|c|}\hline
+    $f_1: y=x^2$   & $f_2: y=1+x^4$        & $f_3: y= x^6$    & $f_4: y=x^3+1$  \\\hline
+    $f_5: y=1-x^2$ & $f_6: y=\frac{1}{x^2}+3$ & $f_7: y= x^{-2}$ & $f_8: y=x^{-2}-2$\\\hline
+    \end{tabular}
+
+  Ordnen Sie zu
+
+  \begin{tabular}{c|c}
+    Funktionsgraph & Funktionsnummer \\\hline
+    $A$ & \LoesungsRaum{$8$}\\\hline
+    $B$ & \LoesungsRaum{$7$}\\\hline
+    $C$ & \LoesungsRaum{$5$}\\\hline
+    $D$ & \LoesungsRaum{$4$}\\\hline
+    $E$ & \LoesungsRaum{$1$}\\\hline
+    $F$ & \LoesungsRaum{$3$}\\\hline
+    \end{tabular}
+  
+  \platzFuerBerechnungen{6.4}
+  (Sie erhalten pro korrekte Zuordnung 0.5 Pkt. Sie erhalten für eine falsche Zuordnung -0.5 Pkt.)
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Potenzfunktion_durch_Punkt_v1.tex

@@ -0,0 +1,12 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+
+  Finden Sie die Funktionsgleichung $y = x^m$, wenn Sie wissen,
+  dass die Funktion durch den Punkt $P=(2 | 64)$ geht.
+
+  
+  Finden Sie den Parameter $m$ und geben Sie die Lösung exakt ($m$ als
+  ganze Zahl oder Bruch) an:
+  $m=\LoesungsRaum{6}$
+  
+  \platzFuerBerechnungen{4.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Potenzfunktion_durch_Punkt_v2.tex

@@ -0,0 +1,14 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Finden Sie die Funktionsgleichung $y = ax^3$, wenn Sie wissen,
+  dass die Funktion durch den Punkt $P=(-3 | 3)$ geht.
+
+  
+  Finden Sie den Parameter $a$ und geben Sie die Lösung exakt ($a$ als Bruch) an:
+
+\leserluft
+  
+  $a=\LoesungsRaum{-\frac19}$
+  
+  \platzFuerBerechnungen{6.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Potenzfunktion_durch_zwei_Punkte_v1.tex

@@ -0,0 +1,15 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Finden Sie die Funktionsgleichung $y = ax^n$, wenn Sie wissen,
+  dass der Graph der Funktion durch die beiden Punkte $P=(2|\frac83)$ und
+  $Q=(-1|\frac16)$ verläuft.
+
+  
+  Finden Sie die Parameter $a$ und $n$ geben Sie die Lösung exakt ($a$ als Bruch) an:
+
+  $a=\LoesungsRaum{\frac16}$
+
+  $n=\LoesungsRaum{4}$
+  
+  \platzFuerBerechnungen{12.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Potenzfunktion_durch_zwei_Punkte_v2.tex

@@ -0,0 +1,15 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Finden Sie die Funktionsgleichung $y = ax^n$, wenn Sie wissen,
+  dass der Graph der Funktion durch die beiden Punkte $P=(-1|-3)$ und
+  $Q=(2|24)$ verläuft.
+
+  
+  Finden Sie die Parameter $a$ und $n$ geben Sie die Lösung exakt ($a$ als Bruch) an:
+
+  $a=\LoesungsRaum{3}$
+
+  $n=\LoesungsRaum{3}$
+  
+  \platzFuerBerechnungen{12.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Spiegelung_v1.tex

@@ -0,0 +1,11 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+  Geben Sie die Symmetrie(en) des Graphen der Funktion
+
+  $$y=x^3$$
+
+  an.
+  
+  \LoesungsRaumLang{Punktspiegelung am Ursprung (0|0).}
+  
+  \platzFuerBerechnungen{4.4}%%
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Spiegelung_v2.tex

@@ -0,0 +1,21 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+  Geben Sie die Symmetrie(en) des Graphen der Funktion
+
+  $$y=x^3$$
+
+  an. Welche der folgenden Spieglungen spiegelt die Funktion $y=x^3$ auf sich selbst ab?
+
+  
+  \wahrbox{falsch} Achsenpiegelung ...
+
+  \wahrbox{wahr} Punktspiegelung ...
+
+  \wahrbox{falsch} ... an der $x$-Achse.
+
+  \wahrbox{falsch} ... an der $y$-Achse.
+
+  \wahrbox{wahr} ... am Ursprung $O=(0 | 0)$.
+  
+  
+  \platzFuerBerechnungen{4.4}%%
+\end{frage}

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/Spiegelung_v3.tex

@@ -0,0 +1,21 @@
+\begin{frage}[1]%% Anzahl Punkte für diese Aufgabe
+  Geben Sie die Symmetrie(en) des Graphen der Funktion
+
+  $$y=x^4$$
+
+  an. Welche der folgenden Spieglungen spiegelt die Funktion $y=x^4$ auf sich selbst ab?
+
+  
+  \wahrbox{wahr} Achsenpiegelung ...
+
+  \wahrbox{falsch} Punktspiegelung ...
+
+  \wahrbox{falsch} ... an der $x$-Achse.
+
+  \wahrbox{wahr} ... an der $y$-Achse.
+
+  \wahrbox{falsch} ... am Ursprung $O=(0 | 0)$.
+  
+  
+  \platzFuerBerechnungen{4.4}%%
+\end{frage}

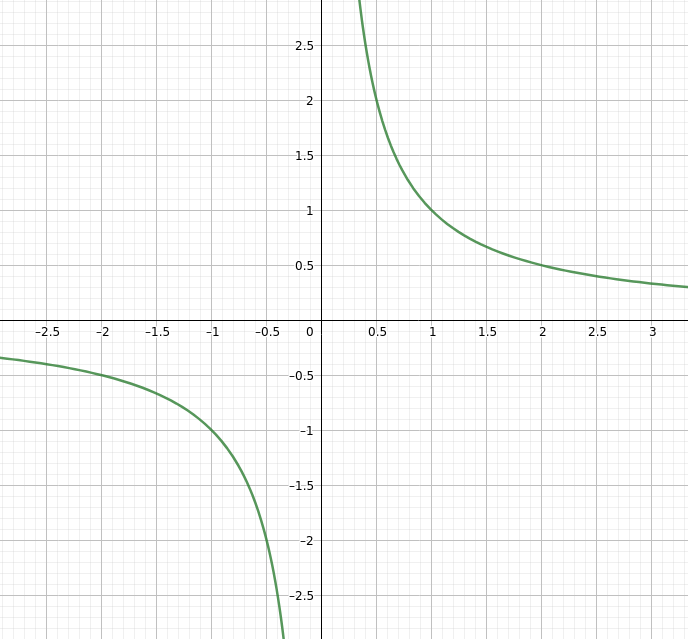
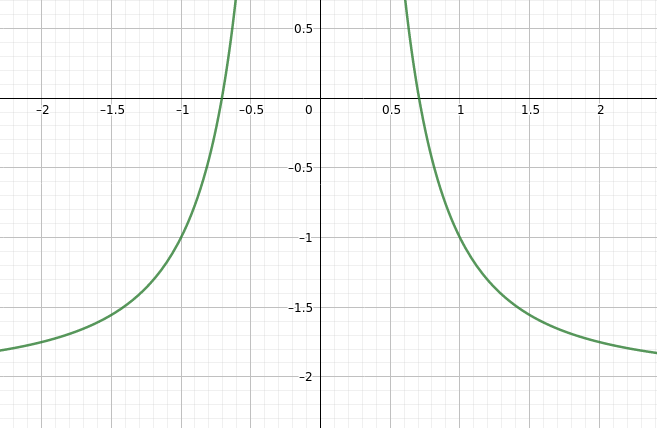
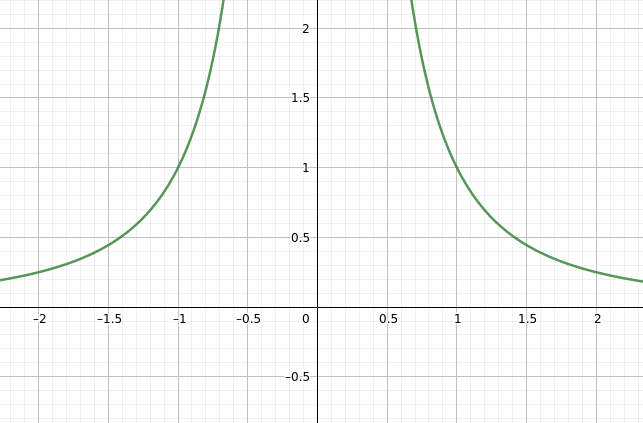
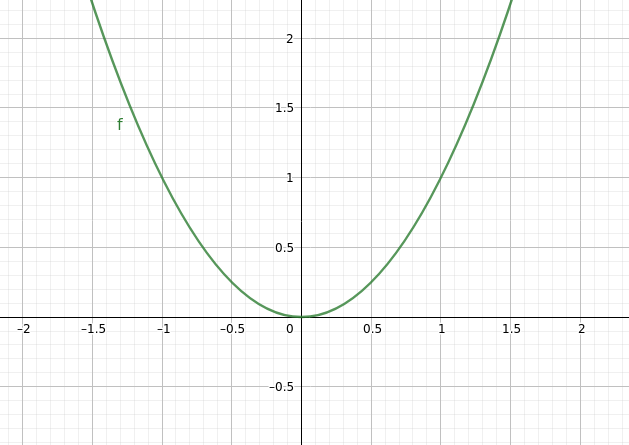
pruefungsAufgaben/P_ALLG/funktionen/potenzfct/potenzfctSkizzieren_p_x_h_4_m1_v2.tex

@@ -0,0 +1,9 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Skizzieren Sie die Funktion
+
+  $$y=-\frac14 x^4 - 1$$
+  
+  \bbwCenterGraphic{6cm}{P_ALLG/funktionen/potenzfct/img/leer.png}
+  \platzFuerBerechnungen{4.4}
+\end{frage} 

pruefungsAufgaben/P_ALLG/funktionen/potenzfct/potenzfctSkizzieren_p_x_h_5_v1.tex

@@ -0,0 +1,6 @@
+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Skizzieren Sie die Funktion $y=-x^5$:
+  \bbwCenterGraphic{6cm}{P_ALLG/funktionen/potenzfct/img/leer.png}
+  \platzFuerBerechnungen{4.4}
+\end{frage} 

pruefungsAufgaben/P_GESO/aa1/addition/Addition_Subtraktion_v1.tex

@@ -0,0 +1,15 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zur Addition und Subtraktion
+%%
+
+\begin{frage}[2]
+  Vereinfachen Sie den folgenden Term:
+  
+  $-(-b - c) - (c - b )$ =  ...................................................\TRAINER{$2b$}\\
+    Notizen:\\
+     \mmPapier{6}
+  
+     \TRAINER{Pro Aufgabe 2 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen Punkt bringen.}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/addition/Addition_Subtraktion_v2.tex

@@ -0,0 +1,24 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zur Addition und Subtraktion
+%%
+
+\begin{frage}[4]
+  Vereinfachen Sie die folgenden Terme:
+
+  a)\\
+  $z+(1-(z+4)+7)+3-(2z-1)$ =  ...................................................\TRAINER{$z^2-z+1$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+  b)\\
+  $am^2 - (3am^2 -a^2m -am^2) - 2am^2$ =
+  ...................................................\TRAINER{$a^2m - 3am^2$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+     \TRAINER{Pro Aufgabe 2 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen Punkt bringen.}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/addition/Addition_Subtraktion_v3.tex

@@ -0,0 +1,38 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zur Addition und Subtraktion
+%%
+
+\begin{frage}[8]
+  Vereinfachen Sie die folgenden Terme:
+
+  a)\\
+  $z+(1-(z+4)+7)+3-(2z-1)$ =  ...................................................\TRAINER{$8-2z$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+  b)\\
+  $am^2 - (3am^2 -a^2m -am^2) - 2am^2$ =
+  ...................................................\TRAINER{$a^2m - 3am^2$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+\newpage
+  c)\\
+  $1-(2-(3-(4-(5-x))))$ =  ...................................................\TRAINER{$3-x$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+    d)\\
+  $12b^3-(6b-(10b^3-3b+2)-10a)$ =  ...................................................\TRAINER{$22b^3 - 9b +2 +10a$}\\
+  \noTRAINER{Notizen:
+    
+     \mmPapier{5}}
+
+  
+     \TRAINER{Pro Aufgabe 2 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen Punkt bringen.}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/addition/Addition_Subtraktion_v4.tex

@@ -0,0 +1,15 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zur Addition und Subtraktion
+%%
+
+\begin{frage}[2]
+  Vereinfachen Sie den folgenden Term:
+  
+  $-(-b - c) - (c - b + (-1))$ =  ...................................................\TRAINER{$2b+1$}\\
+    Notizen:\\
+     \mmPapier{6}%%
+%%  
+     \TRAINER{Pro Aufgabe 2 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen Punkt bringen.}%%
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_Achtung_v1.tex

@@ -0,0 +1,22 @@
+%%
+%% Ausmultiplizieren (ACHTUNG)
+%%
+
+\begin{frage}[3]
+  Schreiben als Summe und vereinfachen Sie so weit wie möglich:
+
+  $$-12(-3 + b) = \LoesungsRaum{36-12b}$$
+  \TRAINER{(1 Pkt)}
+
+  $$8-(-c + 2) = \LoesungsRaum{c + 6}$$
+  \TRAINER{(1 Pkt)}
+
+  $$(a+b+c)s = \LoesungsRaum{as+bs+cs}$$
+  \TRAINER{(1 Pkt)}
+
+
+  Notizen:
+  
+  \noTRAINER{\mmPapier{5.2}}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_Binomische_Formeln_v1.tex

@@ -0,0 +1,24 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[4]
+  Multiplizieren Sie die folgenden Terme aus und vereinfachen Sie (möglicherweise helfen
+  Ihnen die binomischen Formeln):
+  
+
+  $$(2d+3f)^2 = ...........................$$
+  \TRAINER{$4d^2 +12df + 9f^2$ (je 1 Pkt.)}
+
+  $$ (r^2-s)(r^2+s)= .................................$$
+  \TRAINER{$r^4-s^2$}
+  
+  $$ 12b + (b-6)^2 -b^2= .................................$$
+  \TRAINER{$36$}
+  
+  $$ (a-1)^3= .................................$$
+  \TRAINER{$a^3 - 3a^2 + 3a - 1$}
+  
+  \platzFuerTNNotes{12}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_Distributivgesetz_v1.tex

@@ -0,0 +1,28 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[7]
+  Multiplizieren Sie die folgenden Terme aus. Verwenden Sie dazu das
+  Distributivgesetz (oder die binomischen Formeln).
+
+  a) $$(5r)(5r-7) = ...........................$$
+  \TRAINER{$25r^2-35r$ (1 Pkt)}
+  \platzFuerTNNotes{4}
+
+  b)
+  $$(5r-7)(5r+8) = .................................$$
+  \TRAINER{$25r^2+5r-56$ (2 Pkt)}
+  \platzFuerTNNotes{4}
+
+  c)
+   $$ (5r-7)(5r-7) = .................................$$
+  \TRAINER{$25r^2-70r + 49$ (2 Pkt)}
+  \platzFuerTNNotes{4}
+
+  d)
+  $$ (5r-7)(5r+7) = .................................$$
+  \TRAINER{$25r^2-49$ (2 Pkt)}
+  \platzFuerTNNotes{4}
+
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_v1.tex

@@ -0,0 +1,16 @@
+%%
+%% Ausmultiplizieren
+%%
+
+\begin{frage}[3]
+  Multiplizieren Sie die folgenden Terme aus:
+
+  $$3 (x-2a) = ...........................$$
+  \TRAINER{$3x-6a$ (1 Pkt)}
+
+  $$5\cdot(3-2(b-4))c = .................................$$
+  \TRAINER{$55c - 10bc$ (2 Pkt)}
+  
+  \platzFuerTNNotes{6}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_v2.tex

@@ -0,0 +1,17 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[2]
+  Multiplizieren Sie im Folgenden die Klammerterme aus und
+  vereinfachen Sie so weit wie möglich:
+
+  $$5ab^3 - a(+2b^3 - b^3) = ...........................$$
+  \TRAINER{$4ab^3$ (1 Pkt)}
+
+  $$ -2c^2(c^3-c+1) -c(2c^2 -2c) = .................................$$
+  \TRAINER{$-2c^5$ (1 Pkt)}
+  
+  \noTRAINER{\mmPapier{6}}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Ausmultiplizieren_v3.tex

@@ -0,0 +1,23 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[6]
+  Multiplizieren Sie die folgenden Terme aus und fassen Sie danach so
+  weit wie möglich zusammen:
+
+  a)
+  $$5ab^3 - a(+2b^3 - b^3) = ...........................$$
+  \TRAINER{$4ab^3$ (2 Pkt)}
+
+  b)
+  $$ -2c^2(c^3-c+1) -c(2c^2 -2c) = .................................$$
+  \TRAINER{$-2c^5$ (2 Pkt)}
+
+  c)
+   $$ ((a-b)a + b(b-a) - b^2 -2a^2)c - 1 = .................................$$
+  \TRAINER{$-2abc -a^2c - 1$ (2 Pkt)}
+  
+  \platzFuerTNNotes{10}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/BinomeVereinfachen_v1.tex

@@ -0,0 +1,14 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zum Ausmultiplizieren mit binomischen Formeln
+%%
+\begin{frage}[3]%%
+  Vereinfachen Sie den folgenden Term so weit wie möglich:
+  $$\frac{18}{4a}\left(
+\left(\frac{a}{3} + x\right)^2
+-
+\left(\frac{a}{3} - x\right)^2
+\right) = \LoesungsRaumLang{6a}$$
+
+\platzFuerBerechnungen{7.2}%%
+\end{frage}%%

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/BinomeVereinfachen_v1.tex~

@@ -0,0 +1,28 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zum Ausmultiplizieren mit binomischen Formeln
+%%
+\begin{frage}[3]%%
+  Oft vereinfacht sich das Ausmultiplizieren mit der Kenntnis der
+  binomischen Formeln.
+  
+  Multiplizieren Sie aus:
+
+  a)\\
+    $$(3c+2b)^2 =  \LoesungsRaum{9c^2+12bc+4b^2}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}
+
+       b)\\
+    $$(1 - 3x)^2 =  \LoesungsRaum{1 - 6x + 9x^2}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}
+
+     c)\\
+     $$(8a - 1)(8a + 1)   = \LoesungsRaum{64a^2 - 1}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}%%
+%%
+     \TRAINER{Pro Aufgabe 1 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen halben Punkt bringen.}%%
+\end{frage}%%

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/Binome_Ausmultiplizieren_v1.tex

@@ -0,0 +1,28 @@
+%%
+%% Meta: Master Document
+%% Aufgaben zum Ausmultiplizieren mit binomischen Formeln
+%%
+\begin{frage}[3]%%
+  Oft vereinfacht sich das Ausmultiplizieren mit der Kenntnis der
+  binomischen Formeln.
+  
+  Multiplizieren Sie aus:
+
+  a)\\
+    $$(3c+2b)^2 =  \LoesungsRaum{9c^2+12bc+4b^2}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}
+
+       b)\\
+    $$(1 - 3x)^2 =  \LoesungsRaum{1 - 6x + 9x^2}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}
+
+     c)\\
+     $$(8a - 1)(8a + 1)   = \LoesungsRaum{64a^2 - 1}$$\\
+    Notizen:\\
+     \noTRAINER{\mmPapier{4.4}}%%
+%%
+     \TRAINER{Pro Aufgabe 1 Pkt. Bei falscher Lösung kann der
+       Lösungsweg noch einen halben Punkt bringen.}%%
+\end{frage}%%

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/WasBisherGeschah_GESO_v1.tex

@@ -0,0 +1,14 @@
+%%
+%% Aufgaben aus alten Prüfungen (wild gemischt)
+%%
+
+
+%% Ausmultiplizieren (- vor der Klammer?)
+\begin{frage}[1]
+  Ausmultiplizieren (rechnen Sie aus):
+\TRAINER{Lief super: fast präzsie 50\% richtig.}  
+  \leserluft{}
+   $$ -4(7a - 7 - b -7(a - 1)) = \LoesungsRaum{4b}$$
+  \platzFuerBerechnungen{6.8}
+\end{frage}
+

pruefungsAufgaben/P_GESO/aa1/ausmultiplizieren/WasBisherGeschah_GESO_v2.tex

@@ -0,0 +1,14 @@
+%%
+%% Aufgaben aus alten Prüfungen (wild gemischt)
+%%
+
+
+%% Ausmultiplizieren (- vor der Klammer?)
+\begin{frage}[1]
+  Ausmultiplizieren (rechnen Sie aus):
+
+  \leserluft{}
+   $$ 3r - 4(-4-3r)-2(8+7r) = \LoesungsRaum{r}$$
+  \platzFuerBerechnungen{6.0}
+\end{frage}
+

pruefungsAufgaben/P_GESO/aa1/betrag/Betrag_v1.tex

@@ -0,0 +1,16 @@
+%%
+
+\begin{frage}[2]
+  Berechnen Sie die folgenden Ausdrücke:
+
+  \leserluft{}
+
+a)\\
+  $$-\bigg\vert -2 - |-5| \bigg\vert = \LoesungsRaum{-7}$$
+
+b)\\ 
+  $$|-4|\cdot(-3) = \LoesungsRaum{-12}$$
+  
+  \noTRAINER{\mmPapier{3.2}}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/betrag/Betrag_v2.tex

@@ -0,0 +1,23 @@
+%%
+
+\begin{frage}[4]
+  Berechnen Sie die folgenden Ausdrücke:
+
+  \leserluft{}
+
+a)\\
+  $$|7 - 13| =\LoesungsRaum{6}$$
+
+b)\\
+  $$-|28 -3 -28| = \LoesungsRaum{-3}$$
+
+c)\\
+  $$-\bigg\vert -2 - |-5| \bigg\vert = \LoesungsRaum{-7}$$
+
+d)\\ 
+  $$|-4|\cdot(-3) = \LoesungsRaum{-12}$$
+
+\TRAINER{Je 1 Pkt.}
+  \noTRAINER{\mmPapier{3.6}}%%
+\end{frage}
+ 

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Addition_Subtraktion_v1.tex

@@ -0,0 +1,24 @@
+%%
+%% A: Einfache Aufgaben zu Bruchrechnungen
+%%
+
+%% Bruchteme mit Zahlen
+
+\begin{frage}[3]
+  Subtrahieren bzw. addieren Sie die folgenden Bruchterme. Tipp: Bei der zweiten
+  Aufgabe ist es sinnvoll, die Zähler und Nenner vorab so weit wie
+  möglich zu faktorisieren.
+
+  \leserluft{}
+
+  \begin{enumerate}
+  \item $\frac{7}{b-a} - \frac{2}{a-b}$ =
+    .......... \TRAINER{$\frac{9}{b-a}$ (1pkt)}
+  \item $\frac{a^2-2ab+b^2}{a-b} + \frac{a^2-b^2}{a+b}$ =
+    .......... \TRAINER{$2(a-b)=2a-2b$ (2pkt)}
+  \end{enumerate}
+
+  \platzFuerTNNotes{7}
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Addition_Subtraktion_v2.tex

@@ -0,0 +1,29 @@
+%%
+%% A: Einfache Aufgaben zu Bruchrechnungen
+%%
+
+
+\begin{frage}[8]
+  Subtrahieren bzw. addieren Sie die folgenden Bruchterme. Tipp: Oft
+  ist es sinnvoll, die Zähler und Nenner vorab so weit wie
+  möglich zu faktorisieren (oder allenfalls $(-1)$ auszuklammern).
+
+  \leserluft{}
+
+  1. (1 Pkt.: Tipp: erst kürzen)
+  $$\frac{7b}{2b-ab} + \frac{6v}{4v-2av} = .......... $$\TRAINER{$\frac{10}{2-a}$ (1pkt)}
+
+  2. (1 Pkt.: Tipp: in einem der Nenner $-1$ ausklammern)
+  $$\frac{7}{b-a} - \frac{2}{a-b} =  .......... $$\TRAINER{$\frac{9}{b-a}$ (1pkt)}
+
+  3. (2 Pkt.)
+   $$\frac{m}{m-n} - \frac{n}{n-m} - \frac{2mn}{m^2-n^2} =  .......... $$\TRAINER{$\frac{m^2+n^2}{m^2-n^2}$ (2pkt)}
+
+  4. (2 Pkt.)
+  $$\frac{a^2-2ab+b^2}{a-b} + \frac{a^2-b^2}{a+b} =  .......... $$\TRAINER{$2(a-b)=2a-2b$ (2pkt)}
+
+  5. (2 Pkt.)
+  $$\frac{r-1+z}{-r-z} + \frac{r}{r-z} + \frac{z}{z-r} =  .......... $$\TRAINER{$\frac{1}{r+z}$ (2pkt)}
+
+  \platzFuerTNNotes{20}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Addition_Subtraktion_v3.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Einfache Aufgaben zu Bruchrechnungen
+%%
+
+
+\begin{frage}[2]
+  Subtrahieren bzw. addieren Sie die folgenden Bruchterme. Tipp: Oft
+  ist es sinnvoll, die Zähler und Nenner vorab so weit wie
+  möglich zu faktorisieren (oder allenfalls $(-1)$ auszuklammern).
+
+  \leserluft{}
+
+  $$\frac{7}{b-a} - \frac{3}{a-b} =  \LoesungsRaum{\frac{10}{b-a}}$$
+
+  \platzFuerBerechnungen{3.2}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Addition_Subtraktion_v4.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Einfache Aufgaben zu Bruchrechnungen
+%%
+
+
+\begin{frage}[2]
+  Subtrahieren bzw. addieren Sie die folgenden Bruchterme. Tipp: Oft
+  ist es sinnvoll, die Zähler und Nenner vorab so weit wie
+  möglich zu faktorisieren (oder allenfalls $(-1)$ auszuklammern).
+
+  \leserluft{}
+
+  $$\frac{11}{r-t} - \frac{4}{t-r} =  \LoesungsRaum{\frac{15}{r-t} = \frac{-15}{t-r}}$$
+
+  \platzFuerBerechnungen{3.2}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Alte_Maturaaufgabe_v1.tex

@@ -0,0 +1,18 @@
+%%
+%% Alte Maturaaufgabe GESO
+%%
+
+
+
+%% Multiplikation
+\begin{frage}[2]
+  Subtrahieren und vereinfachen Sie:
+
+  \leserluft{}
+
+   $$\frac{5a}{a-4} - \frac{7a}{28-7a} =  \LoesungsRaum{\frac{6a}{a-4}}$$
+  \TRAINER{1.5 pkt, falls einzig Zahlen nicht vollständig gekürzt
+    \zB $\frac{42a}{7(a-4)}$. Hingegen nur noch 0.5 Pkt bei
+    Vorzeichenfehler (\zB $\frac{6a}{4-a}$).}
+\platzFuerBerechnungen{11.2}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Division_v1.tex

@@ -0,0 +1,16 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+
+%% Division
+\begin{frage}[1]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{-x}{y} : \frac{-y}{-x} =\LoesungsRaum{\frac{-x^2}{y^2}}$$
+  \TRAINER{0.5 Pkt für $-\frac{(-x)^2}{y^2}$}
+
+  \platzFuerBerechnungen{3.2}  
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Division_v2.tex

@@ -0,0 +1,15 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+
+%% Division
+\begin{frage}[1]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{-t}{z} : \left(-\frac{t}{-z}\right) =\LoesungsRaum{-1}$$
+
+  \platzFuerBerechnungen{3.2}  
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Binome_v1.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich:
+
+     $$\frac{x^2-16}{x^2+x-20} = \LoesungsRaum{\frac{x+4}{x+5}} $$
+  
+ \platzFuerBerechnungen{3.6} 
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Binome_v2.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich:
+
+     $$\frac{y^2+4y-21}{y^2-9} = \LoesungsRaum{\frac{y+7}{y+3}} $$
+  
+ \platzFuerBerechnungen{3.6} 
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Erweitern_v1.tex

@@ -0,0 +1,60 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[1]
+
+  Kürzen Sie den folgenden Bruch: $\frac{6r - 15}{3}$:
+  ............................
+  \TRAINER{${2r-5}$}
+  
+  \platzFuerTNNotes{2}
+\end{frage}
+
+
+
+\begin{frage}[1]
+  Kürzen Sie die folgenden Brüche so weit wie möglich:
+
+     $$\frac{3a^3b^2x^2y^7}{-30b^2x^5y^2} =
+  ....................$$\TRAINER{$-\frac{a^3y^5}{10x^3}$ (1 Pkt.)}
+  
+  
+  \platzFuerTNNotes{6}
+  
+\end{frage}
+
+
+\begin{frage}[1]
+
+  Kürzen Sie den folgenden Bruch (womöglich hilft das Ausklammern von
+  $(-1)$):
+  
+  \vspace{4mm}
+  
+  $$\frac{rm-rn}{n-m} =  ............................$$
+  \TRAINER{${-r}$}
+
+  \vspace{4mm}
+  
+  \platzFuerTNNotes{3}
+\end{frage}
+
+
+\begin{frage}[1]
+
+  Erweitern Sie den folgenden Bruch mit $(-1)$:
+
+  $$\frac{5-a}{a-2}=\frac{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}{}$$
+
+
+  \TRAINER{${2r-5}$}
+
+    \platzFuerTNNotes{3}
+
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Repetition_v1.tex

@@ -0,0 +1,17 @@
+%%
+%% A: Brüche kürzen (was bisher geschah)
+%%
+
+%%
+
+%% Kürzen
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich
+
+  (Tipp: Beim Kürzen hab' ich mal geschworen, ich streiche immer nur \textbf{Faktoren}!)
+  
+  $$\frac{x^4-1}{x^2-1} =\LoesungsRaum{x^2+1}$$
+
+  \platzFuerBerechnungen{6.8}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Repetition_v2.tex

@@ -0,0 +1,17 @@
+%%
+%% A: Brüche kürzen (was bisher geschah)
+%%
+
+%%
+
+%% Kürzen
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich
+
+  (Tipp: Beim Kürzen hab' ich mal geschworen, ich streiche immer nur \textbf{Faktoren}!)
+  
+  $$\frac{1-b^4}{1-b^2} =\LoesungsRaum{b^2+1}$$
+
+  \platzFuerBerechnungen{7.2}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Repetition_v3.tex

@@ -0,0 +1,17 @@
+%%
+%% A: Brüche kürzen (was bisher geschah)
+%%
+
+%%
+
+%% Kürzen
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich
+
+  (Tipp: Beim Kürzen hab' ich mal geschworen, ich streiche immer nur \textbf{Faktoren}!)
+  
+  $$\frac{x^3-x}{x-1} =\LoesungsRaum{x(x+1) = x^2+x}$$
+
+  \platzFuerBerechnungen{7.2}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Teilsummen_v1.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich:
+
+     $$\frac{ax+a-x-1}{ax-a-x+1} = \LoesungsRaum{\frac{x+1}{x-1}} $$
+  
+ \platzFuerBerechnungen{3.6} 
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_Teilsummen_v2.tex

@@ -0,0 +1,16 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[2]
+  Kürzen Sie den folgenden Bruch so weit wie möglich:
+
+     $$\frac{ay+a-2y-2}{ay+2-2y-a} = \LoesungsRaum{\frac{y+1}{y-1}} $$
+  
+ \platzFuerBerechnungen{3.6} 
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Kuerzen_v1.tex

@@ -0,0 +1,17 @@
+%%
+%% A: Brüche kürzen
+%%
+
+%%
+
+%% Kürzen
+
+
+\begin{frage}[1]
+  Kürzen Sie den folgenden Bruch so weit wie möglich:
+
+     $$\frac{3a^3b^2x^2y^7}{-30b^2x^5y^2} = \LoesungsRaum{-\frac{a^3y^5}{10x^3}} $$
+  
+ 
+ \platzFuerBerechnungen{3.6} 
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Multiplikation_Division_v1.tex

@@ -0,0 +1,124 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+
+
+
+%% Multiplikation
+\begin{frage}[3]
+  Sie können diese Aufgabe auch mit dem Taschenrechner lösen (Je 1 Punkt).
+
+  \vspace{7mm}
+  
+  Wie viel sind $\frac{3}{8}$ von $\frac{4}{9}$?\LoesungsRaum{$\frac{1}{6}$=$\frac{12}{72}$=$1.\overline{6}$=$16.\overline{6}\%$}
+  
+\vspace{5mm}
+
+Wie viel sind $15\%$  von $\frac{13}{45}$?\LoesungsRaum{$0.04333 = \frac{13}{300}=\frac{195}{4500}$}
+
+\vspace{5mm}
+
+
+\vspace{5mm}
+
+Bemerkung: Relative Häufigkeiten werden nicht nur in Prozenten (\%), sondern auch in Häufigkeitsfaktoren angegeben.
+    So ist der Häufigkeitsfaktor ``0.3'' für eine Multiplikation nichts anderes als ``30\%''.
+
+    \vspace{5mm}
+
+    Wie viel sind also $0.125$ von
+    $\frac{16}{3}$?\LoesungsRaum{$\frac{2}{3}$=$0.\overline{6}$=$66.\overline{6}\%$}
+
+    \vspace{5mm}
+    
+  \platzFuerBerechnungen{4}
+\end{frage}
+
+
+
+%% Division
+\begin{frage}[1]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{-x}{y} : \frac{-y}{-x} =\LoesungsRaum{\frac{-x^2}{y^2}}$$
+  \TRAINER{0.5 Pkt für $-\frac{(-x)^2}{y^2}$}
+
+  \platzFuerBerechnungen{3.2}  
+\end{frage}
+
+
+
+%% Division
+\begin{frage}[2]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{4a}{a+3} : \frac{8a^2}{3a+9} = \LoesungsRaum{\frac{3}{2a}}$$
+  \TRAINER{1.5 Pkt. falls nicht vollständig gekürzt. Zum Beispiel $\frac{9a}{6a^2}$}
+
+  \platzFuerBerechnungen{7.2}  
+\end{frage}
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie. Schreiben Sie im Resultat sowohl den
+%  Zähler und den Nenner so weit wie möglich faktorisiert.
+%
+%  $$\frac{x^2-25}{x^4-4} : \frac{x+5}{3x^2-6} = ......................................$$\TRAINER{$\frac{3(x-5)(x-1)(x+1)}{(x^2-2)(x^2+2)}$}
+%  
+%\platzFuerTNNotes{8}  
+%\end{frage}
+
+
+
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term:
+% 38c Marthaler Algebra  abgeändernt
+%  $$\left(a^3-\frac{a^4}{m^2}\right) : \frac{a^2}{-m}=\LoesungsRaum{\frac{a(a-m^2)}{m}}$$
+%  \TRAINER{Für nicht gekürzt nur 0.5 Pkt}
+%  \platzFuerBerechnungen{6}
+%\end{frage}
+
+
+\begin{frage}[2]
+  Multiplizieren und vereinfachen Sie den folgenden Term:
+  \leserluft{}
+%% Marhtaler Algebra abgeändert
+  $$ \frac{r-1}{-24a} \cdot \frac{8a^2}{1-r}=\LoesungsRaum{\frac{a}{3}}$$
+  \TRAINER{-a/3 = 0 Pkt. ; Zahl nicht vollständig gekürzt 1.5 Pkt
+    ($\frac{8a}{24}$). $a$ nicht vollständig gekürtz noch 1 Pkt
+    ($\frac{a^2}{3a}$). Hingegen $\frac{-a}{-3}$ sind auch 1.5 Pkt.}
+  \platzFuerBerechnungen{6}
+\end{frage}
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term:
+  
+%% Marhtaler Algebra abgeändert
+%  $$ \left(-7s - 14t\right) : \frac{2t+s}{2t}= ......................................$$\TRAINER{$???$}
+  
+%  \platzFuerBerechnungen{6}
+%\end{frage}
+
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term (Tipp, erst kürzen, wo möglich):
+%  
+%%% Marhtaler Algebra abgeändert
+%  $$ \frac{x^2 + y^2}{x-y} : \frac{x^2 - y^2}{x+y}= ......................................$$\TRAINER{$???$}
+%  
+%  \platzFuerTNNotes{8}
+%\end{frage}
+
+
+\begin{frage}[1]
+  Vereinfachen Sie den folgenden Ausdruck:
+%% Alte Gymmi-Aufnahmeprüfung nach 2. Sek
+  $$ \frac{9a+14}{6a} - \frac{7b}{3a^2}:\frac{b}{a}=\LoesungsRaum{\frac{3}{2}}$$
+  
+  \platzFuerBerechnungen{6}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Multiplikation_Division_v2.tex

@@ -0,0 +1,124 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+
+
+
+%% Multiplikation
+\begin{frage}[3]
+  Sie können diese Aufgabe auch mit dem Taschenrechner lösen (Je 1 Punkt).
+
+  \vspace{7mm}
+  
+  Wie viel sind $\frac{3}{8}$ von $\frac{4}{9}$?\LoesungsRaum{$\frac{1}{6}$}
+  
+\vspace{5mm}
+
+Wie viel sind $15\%$  von $\frac{13}{45}$?\LoesungsRaum{$0.04333 = \frac{13}{300}=\frac{195}{4500}$}
+
+\vspace{5mm}
+
+
+\vspace{5mm}
+
+Bemerkung: Relative Häufigkeiten werden nicht nur in Prozenten (\%), sondern auch in Häufigkeitsfaktoren angegeben.
+    So ist der Häufigkeitsfaktor ``0.3'' für eine Multiplikation nichts anderes als ``30\%'' (1Pkt).
+
+    \vspace{5mm}
+
+    Wie viel sind also $0.125$ von $\frac{16}{3}$?\LoesungsRaum{$\frac{2}{3}$}
+
+    \vspace{5mm}
+    
+  \platzFuerBerechnungen{4}
+\end{frage}
+
+
+
+%% Division
+\begin{frage}[1]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{-x}{y} : \frac{-y}{-x} =\LoesungsRaum{\frac{-x^2}{y^2}}$$
+  \TRAINER{0.5 Pkt für $-\frac{(-x)^2}{y^2}$}
+
+  \platzFuerBerechnungen{3.2}  
+\end{frage}
+
+
+
+%% Division
+\begin{frage}[2]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{4a}{a+3} : \frac{8a^2}{3a+9} = \LoesungsRaum{\frac{3}{2a}}$$
+  \TRAINER{1.5 Pkt. falls nicht vollständig gekürzt. Zum Beispiel $\frac{9a}{6a^2}$}
+
+  \platzFuerBerechnungen{7.2}  
+\end{frage}
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie. Schreiben Sie im Resultat sowohl den
+%  Zähler und den Nenner so weit wie möglich faktorisiert.
+%
+%  $$\frac{x^2-25}{x^4-4} : \frac{x+5}{3x^2-6} = ......................................$$\TRAINER{$\frac{3(x-5)(x-1)(x+1)}{(x^2-2)(x^2+2)}$}
+%  
+%\platzFuerTNNotes{8}  
+%\end{frage}
+
+
+
+
+
+\begin{frage}[2]
+  Dividieren und vereinfachen Sie den folgenden Term:
+ 38c Marthaler Algebra  abgeändernt
+  $$\left(a^3-\frac{a^4}{m^2}\right) : \frac{a^2}{-m}=\LoesungsRaum{\frac{a(a-m^2)}{m}}$$
+  \TRAINER{Für nicht gekürzt nur 0.5 Pkt
+    \zB $\frac{-a^3m^3+a^4m}{m^2a^2}$ etc.}
+  \platzFuerBerechnungen{6}
+\end{frage}
+
+
+\begin{frage}[2]
+  Multiplizieren und vereinfachen Sie den folgenden Term:
+  
+%% Marhtaler Algebra abgeändert
+  $$ \frac{r-1}{-24a} \cdot\frac{8a^2}{1-r}=\LoesungsRaum{\frac{a}{3}}$$
+  \TRAINER{Für falsches Vorzeichen 0.5 Pkt. Für nicht vollständig
+    gekürzt 1Pkt. Falls einzig $\frac{-a}{-3}$ dastehet: 1.5
+    Pkt. Alles andere 0 Pkt.}
+  \platzFuerBerechnungen{6}
+\end{frage}
+
+
+\begin{frage}[2]
+  Dividieren und vereinfachen Sie den folgenden Term:
+  
+% Marhtaler Algebra abgeändert
+  $$ \left(-7s - 14t\right) : \frac{2t+s}{2t}= \LoesungsRaum{-14t}$$
+  
+  \platzFuerBerechnungen{6}
+\end{frage}
+
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term (Tipp, erst kürzen, wo möglich):
+%  
+%%% Marhtaler Algebra abgeändert
+%  $$ \frac{x^2 + y^2}{x-y} : \frac{x^2 - y^2}{x+y}= ......................................$$\TRAINER{$???$}
+%  
+%  \platzFuerTNNotes{8}
+%\end{frage}
+
+
+\begin{frage}[1]
+  Vereinfachen Sie den folgenden Ausdruck:
+%% Alte Gymmi-Aufnahmeprüfung nach 2. Sek
+  $$ \frac{9a+14}{6a} - \frac{7b}{3a^2}:\frac{b}{a}=\LoesungsRaum{\frac{3}{2}}$$
+  \TRAINER{Falls nicht vollständig gekürtz: 0.5 Pkt.}
+  \platzFuerBerechnungen{6}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Multiplikation_Division_v3.tex

@@ -0,0 +1,126 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+
+
+
+
+
+%% Division
+\begin{frage}[1]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{-r}{b} : \frac{-b}{-r} =\LoesungsRaum{\frac{-r^2}{b^2}}$$
+  \TRAINER{0.5 Pkt für $-\frac{(-r)^2}{b^2}$}
+
+  \platzFuerBerechnungen{3.2}  
+\end{frage}
+
+%% Multiplikation
+\begin{frage}[3]
+  Sie können diese Aufgabe auch mit dem Taschenrechner lösen (Je 1 Punkt).
+
+  \vspace{7mm}
+  
+  Wie viel sind $\frac{9}{8}$ von $\frac{4}{3}$?\LoesungsRaum{$1.5$}
+  
+\vspace{5mm}
+
+Wie viel sind $45\%$  von $\frac{13}{15}$?\LoesungsRaum{$0.39$}
+
+\vspace{5mm}
+
+
+\vspace{5mm}
+
+Bemerkung: Relative Häufigkeiten werden nicht nur in Prozenten (\%), sondern auch in Häufigkeitsfaktoren angegeben.
+    So ist der Häufigkeitsfaktor ``0.3'' für nichts anderes als ``30\%''.
+
+    \vspace{5mm}
+
+    Wie viel sind also $0.375$ von
+    $\frac{16}{3}$?\LoesungsRaum{$2$}
+
+    \vspace{5mm}
+    
+  \platzFuerBerechnungen{4}
+\end{frage}
+
+
+
+%% Division
+\begin{frage}[2]
+  Dividieren und vereinfachen Sie:
+
+  $$\frac{4a}{a+3} : \frac{8a^2}{3a+9} = \LoesungsRaum{\frac{3}{2a}}$$
+  \TRAINER{1.5 Pkt. falls nicht vollständig gekürzt. Zum Beispiel $\frac{9a}{6a^2}$}
+
+  \platzFuerBerechnungen{7.2}  
+\end{frage}
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie. Schreiben Sie im Resultat sowohl den
+%  Zähler und den Nenner so weit wie möglich faktorisiert.
+%
+%  $$\frac{x^2-25}{x^4-4} : \frac{x+5}{3x^2-6} = ......................................$$\TRAINER{$\frac{3(x-5)(x-1)(x+1)}{(x^2-2)(x^2+2)}$}
+%  
+%\platzFuerTNNotes{8}  
+%\end{frage}
+
+
+
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term:
+% 38c Marthaler Algebra  abgeändernt
+%  $$\left(a^3-\frac{a^4}{m^2}\right) : \frac{a^2}{-m}=\LoesungsRaum{\frac{a(a-m^2)}{m}}$$
+%  \TRAINER{Für nicht gekürzt nur 0.5 Pkt}
+%  \platzFuerBerechnungen{6}
+%\end{frage}
+
+
+\begin{frage}[2]
+  Multiplizieren und vereinfachen Sie den folgenden Term vollständig:
+  \leserluft{}
+  %% Marhtaler Algebra abgeändert
+  
+  $$ \frac{r-1}{-24a} \cdot \frac{8a^2}{1-r}=\LoesungsRaum{\frac{a}{3}}$$
+
+  \TRAINER{-a/3 = 0 Pkt. ; Zahl nicht vollständig gekürzt 1.5 Pkt
+    ($\frac{8a}{24}$). $a$ nicht vollständig gekürtzt noch 1 Pkt
+    ($\frac{a^2}{3a}$). Hingegen $\frac{-a}{-3}$ sind auch 1.5 Pkt.}
+  \platzFuerBerechnungen{6}
+\end{frage}
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term:
+  
+%% Marhtaler Algebra abgeändert
+%  $$ \left(-7s - 14t\right) : \frac{2t+s}{2t}= ......................................$$\TRAINER{$???$}
+  
+%  \platzFuerBerechnungen{6}
+%\end{frage}
+
+
+
+%\begin{frage}[2]
+%  Dividieren und vereinfachen Sie den folgenden Term (Tipp, erst kürzen, wo möglich):
+%  
+%%% Marhtaler Algebra abgeändert
+%  $$ \frac{x^2 + y^2}{x-y} : \frac{x^2 - y^2}{x+y}= ......................................$$\TRAINER{$???$}
+%  
+%  \platzFuerTNNotes{8}
+%\end{frage}
+
+
+\begin{frage}[1]
+  Vereinfachen Sie den folgenden Ausdruck:
+%% Alte Gymmi-Aufnahmeprüfung nach 2. Sek
+  $$ \frac{9a+14}{6a} - \frac{7b}{3a^2}:\frac{b}{a}=\LoesungsRaum{\frac{3}{2}}$$
+  
+  \platzFuerBerechnungen{6}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_Multiplikation_v1.tex

@@ -0,0 +1,14 @@
+%%
+%% B: Aufgaben zu Bruchrechnungen
+%%
+
+\begin{frage}[2]
+  Multiplizieren und vereinfachen Sie den folgenden Term:
+  
+%% Marhtaler Algebra abgeändert
+  $$ \frac{r-1}{-24a} \cdot\frac{8a^2}{1-r}=\LoesungsRaum{\frac{a}{3}}$$
+  \TRAINER{Für falsches Vorzeichen 0.5 Pkt. Für nicht vollständig
+    gekürzt 1Pkt. Falls einzig $\frac{-a}{-3}$ dastehet: 1.5
+    Pkt. Alles andere 0 Pkt.}
+  \platzFuerBerechnungen{6}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/Bruchrechnen_v1.tex

@@ -0,0 +1,23 @@
+%%
+%% A: Einfache Aufgaben zu Bruchrechnungen
+%%
+
+%% Bruchteme mit Zahlen
+\begin{frage}[2]
+  Berechnen Sie die folgenden Bruchterme (wer nicht geübt im
+  Kopfrechnen ist, kann hier den TI-30X Pro MathPrint verwenden.):
+
+  \leserluft{}
+
+  \begin{itemize}
+  \item $\frac{7}{4} \cdot \frac{2}{3}$ =
+    .......... \TRAINER{$\frac{14}{12} = \frac{7}{6}$ (1p)}
+  \item $\frac{7}{4} : \frac{2}{3}$ =
+    .......... \TRAINER{$\frac{21}{8}$ (0.5 pt.)}
+  \item $\frac{7}{4} + \frac{2}{3}$ =
+    .......... \TRAINER{$\frac{21+8}{12}=\frac{29}{12}$ (0.5pt)}
+  \end{itemize}
+  
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/WasBisherGeschah_GESO_v6.tex

@@ -0,0 +1,15 @@
+%%
+%% Aufgaben aus alten Prüfungen (wild gemischt)
+%%
+
+
+%% Zweiklammeransatz
+\begin{frage}[1]
+  Vereinfachen Sie den folgenden Bruchterm so weit wie möglich:
+
+  \leserluft{}
+
+  $$\frac{a-1}{1-a^2} = \LoesungsRaum{\frac{-1}{1+a}}$$
+  
+\platzFuerBerechnungen{6.8}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/bruchrechnen/aufgabenKuerzenErweiternGESO.txt

@@ -0,0 +1,23 @@
+Aufgaben zum Kürzen und Erweitern (GESO)
+=======================================
+Buch Marthaler
+
+
+S48ff
+Terme: Aufg. 2. d)
+
+Definitionsbreicht: 3. c) d)
+
+Kürzen:
+ 5. d)
+ 6. a)
+ 7. a) b)
+ 8. b) d) f)
+ 9. a) c) h)
+10. b)
+11./12. beliebig 2-4 Aufgaben als Training
+
+Erweitern:
+14. a) c)
+15. a) c)
+16. a) b) c)

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Alles_Zusammen_v1.tex

@@ -0,0 +1,14 @@
+%%
+%% Ausklammern, vermischte Aufgaben
+%%
+
+\begin{frage}[3]
+  Klammern Sie so weit wie möglich aus. Verwenden Sie zunächst die
+  zweite, danach die dritte binomische Formel:
+
+  $$p^2 - 4pq + 4q^2 - s^2 = ...........................$$
+  \TRAINER{$(p-2q+s)(p-2q-s)$ (3 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Binomische_Formeln_v1.tex

@@ -0,0 +1,21 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[3]
+  Klammern Sie in den folgenden Summen so viel wie möglich aus.
+  Verwendenen Sie am Besten die erste, die zweite bzw. die dritte
+  binomische Formel.
+
+  $$81x^2 + 72x + 16 =
+  ...........................$$\TRAINER{$(9x+4)^2$ (1 Pkt.)}
+
+  $$25r^2 -30r +9 = ...........................$$\TRAINER{$(5r-3)^2$ (1 Pkt.)}
+
+  $$49z^2 - 64v^2 =
+  ...........................$$\TRAINER{$(7z+8v)(7z-8v)$ (1 Pkt.)}
+  
+  
+  \platzFuerTNNotes{10}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Binomische_Formeln_v2.tex

@@ -0,0 +1,14 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[1]
+  Faktorisieren Sie!
+  Verwendenen Sie am besten die erste, die zweite oder die dritte
+  binomische Formel.
+
+  $$81x^2 + 72x + 16 = \LoesungsRaum{(9x+4)^2}$$
+  
+  \platzFuerBerechnungen{4.0}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Binomische_Formeln_v3.tex

@@ -0,0 +1,12 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[3]
+  Verwandeln Sie die folgende Differenz (bzw. Summe mit negativen Summanden) mit Hilfe der binomischen Formeln in ein Produkt.
+
+  $$m^2 -6mn + 9n^2 -1 = \LoesungsRaum{(m-3n+1)(m-3n-1)}$$
+  
+  \platzFuerBerechnungen{4.0}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Binomische_Formeln_v4.tex

@@ -0,0 +1,14 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[1]
+  Faktorisieren Sie!
+  Verwendenen Sie am besten die erste, die zweite oder die dritte
+  binomische Formel.
+
+  $$25x^2 + 90x + 81 = \LoesungsRaum{(5x+9)^2}$$
+  
+  \platzFuerBerechnungen{4.0}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Binomische_Formeln_v5.tex

@@ -0,0 +1,12 @@
+%%
+%% Ausmultiplizieren (ohne Binomische Formeln)
+%%
+
+\begin{frage}[3]
+  Verwandeln Sie die folgende Differenz (bzw. Summe mit negativen Summanden) mit Hilfe der binomischen Formeln in ein Produkt.
+
+  $$r^2 - 4rt + 4t^2 - 1 = \LoesungsRaum{(r-2t-1)\cdot{}(r-2t+1)}$$
+  
+  \platzFuerBerechnungen{4.0}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Gemeinsame_Faktoren_v1.tex

@@ -0,0 +1,26 @@
+%%
+%% Ausklammern
+%%
+
+\begin{frage}[1]
+  Klammern Sie in der folgenden Summe den größtmöglichen Faktor
+  aus. Tipp: Testen Sie Ihr Resultat durch Ausmultiplizieren.
+
+  $$4ab-8bc+20bd-4b^2 = ...........................$$
+  \TRAINER{$4b(a-2c+5d-b)$ (1 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+
+
+\begin{frage}[1]
+  Klammern Sie aus:
+
+  $$a^9 + a^3 = ...........................$$
+  \TRAINER{$a^3(a^6+1)$ (1 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Gemeinsame_Faktoren_v2.tex

@@ -0,0 +1,13 @@
+%%
+%% Ausklammern
+%%
+
+\begin{frage}[1]
+  Klammern Sie in der folgenden Summe den größtmöglichen Faktor
+  aus.
+
+  $$4ab-8bc+20bd-4b^2 + 12b= \LoesungsRaum{4b(a-2c+5d-b+3)}$$
+
+  \platzFuerBerechnungen{3.6}
+\end{frage}
+

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Gemeinsame_Faktoren_v3.tex

@@ -0,0 +1,15 @@
+%%
+%% Ausklammern
+%%
+
+\begin{frage}[1]
+  Klammern Sie in der folgenden Summe den größtmöglichen Faktor
+  aus. Tipp: Testen Sie Ihr Resultat durch Ausmultiplizieren.
+
+  $$4ab-8bc+20bd-4b^2 = ...........................$$
+  \TRAINER{$4b(a-2c+5d-b)$ (1 Pkt)}
+
+  \platzFuerBerechnungen{4.4}
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_MinusEins_v1.tex

@@ -0,0 +1,13 @@
+%%
+%% Ausklammern, vermischte Aufgaben
+%%
+
+\begin{frage}[2]
+  Klammern Sie so weit wie möglich aus:
+
+  $$r(5-p) - 15 + 3p = ...........................$$
+  \TRAINER{$(r-3)(5-p)$ (2 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Teilsummen_Bilden_v1.tex

@@ -0,0 +1,24 @@
+%%
+%% Ausmultiplizieren (ohne binomische Formeln)
+%%
+
+\begin{frage}[6]
+  Klammern Sie die folgenden Terme aus. Erzeugen Sie zunächst
+  identische Klammerterme indem Sie aus Teilsummen ausklammmern
+  (Teilsummen ausklammern):
+
+  a)
+  $$12bx-4xy-21ab+7ay = ...........................$$
+  \TRAINER{$(4x-7a)(3b-y)$ (1 Pkt)}
+
+  b)
+  $$ any + bmx + amx + bny + bmy + bnx + anx + amy = .................................$$
+  \TRAINER{$(a+b)(m+n)(x+y)$ (2 Pkt)}
+
+  c)
+   $$(3m+4)(3a-2c) + 16c + (6-3m)(3a-2c) - 24a = ...........................$$
+  \TRAINER{$2(3a-2c)$ (3 Pkt)}
+
+  \platzFuerTNNotes{24}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Teilsummen_v1.tex

@@ -0,0 +1,26 @@
+%%
+%% Ausklammern mit gemeinsamen Klammerausdrücken
+%%
+
+\begin{frage}[1]
+  Klammern Sie aus:
+
+  $$ 5(r-t) + b(r-t)= ...........................$$
+  \TRAINER{$(5+b)(r-t)$ (1 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+
+
+\begin{frage}[1]
+
+  Klammern Sie aus:
+  $$b(4ax-4ay) - x + y = ...........................$$
+  \TRAINER{$(4ab-1)(x-y)$ (1 Pkt)}
+
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Teilsummen_v2.tex

@@ -0,0 +1,29 @@
+%%
+%% Ausmultiplizieren (ohne binomische Formeln)
+%%
+
+\begin{frage}[8]
+  Klammern Sie die folgenden Terme aus. Erzeugen Sie zunächst
+  identische Klammerterme indem Sie aus Teilsummen ausklammmern
+  (Teilsummen ausklammern):
+
+  a)
+  $$12bx-4xy-21ab+7ay = ...........................$$
+  \TRAINER{$(4x-7a)(3b-y)$ (2 Pkt)}
+
+  b)
+  
+  $$(4ax-4ay)b - x + y = ...........................$$
+  \TRAINER{$(4ab-1)(x-y)$ (1 Pkt)}
+
+  c)
+  $$ any + bmx + amx + bny + bmy + bnx + anx + amy = .................................$$
+  \TRAINER{$(a+b)(m+n)(x+y)$ (2 Pkt)}
+
+  d)
+   $$(3m+4)(3a-2c) + 16c + (6-3m)(3a-2c) - 24a = ...........................$$
+  \TRAINER{$2(3a-2c)$ (3 Pkt)}
+
+  \platzFuerTNNotes{24}
+\end{frage}
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Ausklammern_Zweiklammeransatz_v1.tex

@@ -0,0 +1,32 @@
+%%
+%% Ausklammern, Zweiklammeransatz
+%%
+
+\begin{frage}[2]
+  Klammern Sie so weit wie möglich aus (eventuell hilft der Zweiklammeransatz):
+
+  $$x^2-9x+20 = ...........................$$
+  \TRAINER{$(x-4)(x-5)$ (2 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+
+\begin{frage}[2]
+  Faktorisieren Sie zunächst mit Hilfe des Taschenrechners die Zahl
+  1\,517 (Tippen Sie 1\,517 \fbox{math} «Pfactor» \fbox{enter}\,\fbox{enter}).
+
+  $$1\,517 = ...... \cdot .....$$
+
+  Faktorisieren Sie nun den folgenden Ausdruck mit dem
+  Zweiklammeransatz:
+  
+  $$x^2  - 4x - 1\,517 =  ...............$$
+  \TRAINER{$(x - 41)(x + 37)$ (2 Pkt)}
+
+  \platzFuerTNNotes{4}
+\end{frage}
+
+
+
+  

pruefungsAufgaben/P_GESO/aa1/faktorisieren/Faktorisieren_v1.tex

@@ -0,0 +1,26 @@
+%%
+%% Meta: Master Document
+%% Einfache Aufgaben zu Termen
+%%
+
+\begin{frage}[3]
+	Multiplizieren Sie die folgenden Faktoren aus:
+	\begin{enumerate}[label=\alph*)]
+		\item $3(7a-2) = $               \TRAINER{Lsg.: $21a - 6$}
+		\item $3(a+b)(c-d)z = $          \TRAINER{Lsg.: $3acz - 3adz + 3bcz - 3bdz$}
+		\item $(s-t)(s+t)(s^2 + t^2) = $ \TRAINER{Lsg.: $s^4 - t^4$}
+	\end{enumerate}
+\platzFuerTNNotes{8}
+\end{frage}
+
+
+\begin{frage}[3]
+	Faktorisieren Sie die folgenden Terme (ausklammern):
+
+	\begin{enumerate}[label=\alph*)]
+		\item $14x - 28z + 42y = $             \TRAINER{Lsg.: $14(x+3y-2z)$}
+		\item $12sorte - 18rose = $            \TRAINER{Lsg.: $6sore(2t - 3)$}
+		\item $m(ab - 4) - (4 -ab)\cdot z = $  \TRAINER{Lsg.: $(m+z)(ab-4)$}
+	\end{enumerate}
+	\platzFuerTNNotes{7}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/faktorisieren/WasBisherGeschah_Faktorisieren_v1.tex

@@ -0,0 +1,12 @@
+%%
+%% Meta: Master Document
+%% Repetitionsaufgabe zum Faktorisieren
+%%
+
+\begin{frage}[2]
+	Kürzen Sie so weit wie möglich:
+  $$\frac{x^2-1}{x-1}=\LoesungsRaum{x+1}$$
+
+  \platzFuerBerechnungen{3.6}
+\end{frage}
+

pruefungsAufgaben/P_GESO/aa1/faktorisieren/WasBisherGeschah_GESO_v1.tex

@@ -0,0 +1,14 @@
+%%
+%% Aufgaben aus alten Prüfungen (wild gemischt)
+%%
+
+%% Zweiklammeransatz
+\begin{frage}[1]
+  Faktorisieren Sie den folgenden Term:
+
+  \leserluft{}
+
+   $$ x^2 -5x - 24 =\LoesungsRaum{(x-8)(x+3)}$$
+  
+\platzFuerBerechnungen{6.8}
+\end{frage}

pruefungsAufgaben/P_GESO/aa1/faktorisieren/WasBisherGeschah_GESO_v3.tex

@@ -0,0 +1,14 @@
+%%
+%% Aufgaben aus alten Prüfungen (wild gemischt)
+%%
+
+
+%% Ausklammern
+\begin{frage}[1]
+  Klammern Sie so viel wie möglich aus:
+
+  \leserluft{}
+   $$ 15a^9 + 10a^3 = \LoesungsRaum{5a^3(3a^6+2)}$$
+  \platzFuerBerechnungen{6.0}
+\end{frage}
+