Ver código fonte
Kleider Bügel Haken Aufgabe neu formuliert
4 arquivos alterados com 12 adições e 6 exclusões
+ 12
- 6
aufgaben/P_GESO/stoch/kombinatorik/Kombinatorik_kombiniert_Kleiderhaken_v1.tex
Ver arquivo
|
||
| 1 | 1 |
|
| 2 |
|
|
| 3 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 | 4 |
|
| 5 | 5 |
|
| 6 |
|
|
| 7 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 8 | 9 |
|
| 9 | 10 |
|
| 10 | 11 |
|
| 12 |
|
|
| 13 |
|
|
| 14 |
|
|
| 15 |
|
|
| 16 |
|
|
| 11 | 17 |
|
| 12 | 18 |
|
| 13 |
|
|
| 14 |
|
|
| 19 |
|
|
| 20 |
|
|
| 15 | 21 |
|
| 16 | 22 |
|
| 17 | 23 |
|
BIN
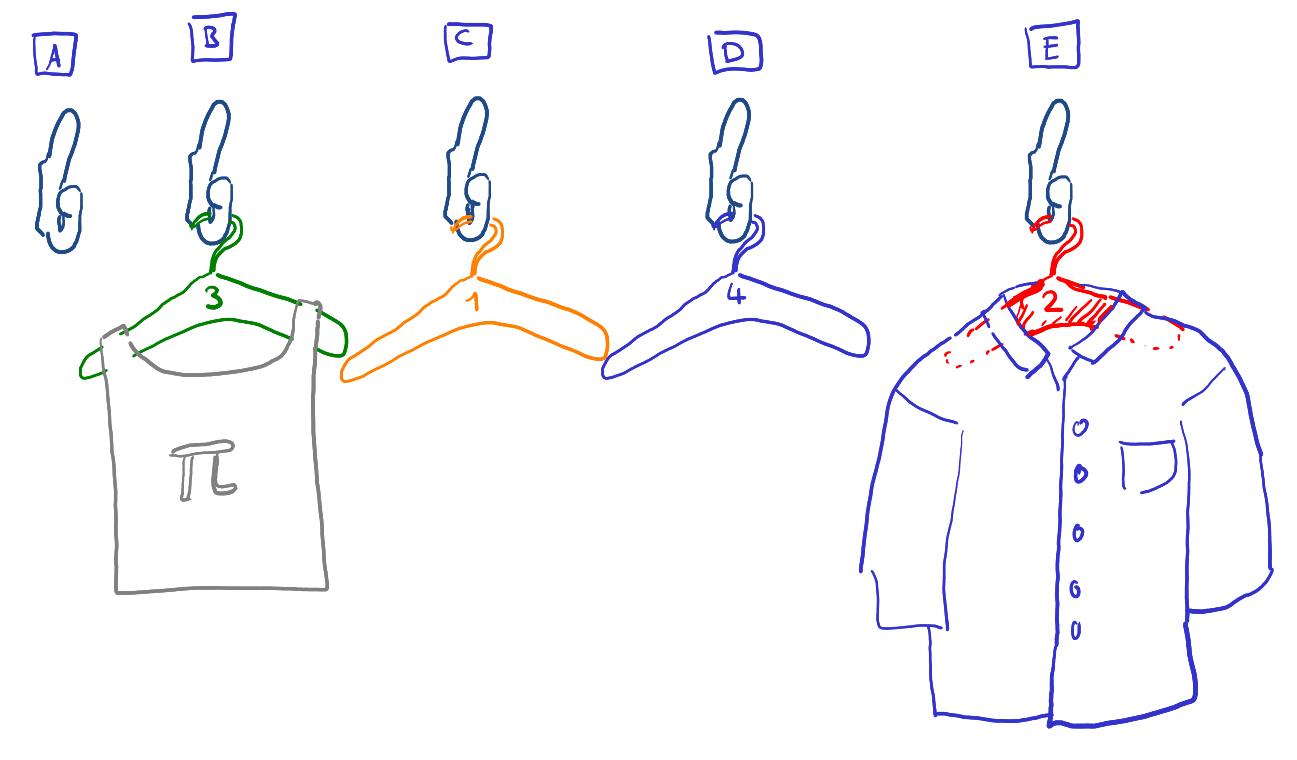
aufgaben/P_GESO/stoch/kombinatorik/img/HakenBuegelKleider.png
Ver arquivo
BIN
aufgaben/P_GESO/stoch/kombinatorik/img_src/HakenBuegelKleider.xopp
Ver arquivo
BIN
aufgaben/P_GESO/stoch/kombinatorik/img_src/HakenBuegelKleider.xopp~
Ver arquivo
Carregando…
