Prüfungsfragen zu Polynomfunktionen

21_22_B/6MT19c_pr4_Polynomfunktionen/.gitignore

+*.pdf

21_22_B/6MT19c_pr4_Polynomfunktionen/Lernziele.txt

+Polynomfunktionen
+
+
+Kehren Sie die folgenden Funktionen um (finden Sie eine Umkehrfunktion):
+
+f(x) = x³+1    (haben wir schon in der Stunde gemacht)
+f(x) = x²-2    (Achtung: Warum ist diese Funktion nicht auf dem ganzen
+                Definitionsbereich umkehrbar?)
+                           (Lösung: Verschiedene x-Werte erzielen dasselbe y)
+f(x) = sin(x)  (Auch der Sinus kann nur stückweise umgekehrt werden!)
+
+Aus dem Lehrbuch (Taschenrechner, Geogebra helfen hier):
+Zeichnen Sie bis Aufg. 805 jeweils √ bzw. n-te √ auch ein:
+S. 213 ff: Auf 803. n), 804. h), 805. c), 806. c), 807. a) c), 808. b)
+
+Aus den Strukturaufgaben (Schwerpunktfach (SPF)):
+Aufg. 46. (Tipp: Funktionen gleichsetzen, solver, danach schauen, dass
+beide Lösungen identisch werden)
+und Aufg 50. (Auch Taschenrechner: Wie immer 1. Funktion definieren
+f(x):= ..., 2. Punkte einsezten und Gleichugssystem
+aufstellen. 3. Gleichungssystem lösen. Dies ergibt die Parameter m und k).
+
+
+Lernziele für die freiwillige Prüfung:
+* Polynomfunktionen:
+   -> Graph aus Funktionsterm skizzieren
+   -> Funktionsterm ab Graph ablesen
+* Erkennen einfacher, doppelter und dreifacher Nullstellen.
+* Charakteristische Punkte (auch Wendepunkte) erkennen und angeben
+können
+* Polynom-Ungleichungen 
+
+ 

21_22_B/6MT19c_pr4_Polynomfunktionen/Pruefung.tex

+
+%%
+%% Schwerpunktfach Algebra II
+%% Potenzgesetze
+%%
+
+\input{bbwLayoutPruefung}
+
+
+\renewcommand{\pruefungsThema}{Polynomfunktionen}
+\renewcommand{\klasse}{6c}
+\renewcommand{\pruefungsNummer}{4}
+\renewcommand{\pruefungsTeil}{...mit TR}
+\renewcommand{\pruefungsDatum}{Mi., 15. Juni 2022}
+%% TALS MIT TR * 2.5
+%% TALS OHNE TR * 3.5
+%% GESO * 4
+\renewcommand{\pruefungsVorgabeZeit}{50 Minuten}%% ich braucthe 14  (Faktor 3.5)
+\renewcommand{\achtAvier}{open Book}
+\renewcommand{\pruefungsHilfsmittel}{\defaultHiflsmittelMitRechner}
+
+\begin{document}%%
+\pruefungsIntro{}
+
+\section{Polynomfunktionen}
+\input{P_TALS/fct3/polynomfunktionen/Punkte_benennen_v1}
+\input{P_TALS/fct3/polynomfunktionen/Grad4_skizzieren_v1}
+\input{P_TALS/fct3/polynomfunktionen/Grad5_ablesen_v1}
+\input{P_TALS/fct3/polynomfunktionen/AbTextbeschreibung_v1}
+\input{P_TALS/fct3/polynomfunktionen/GeradeAbTextbeschreibung_v1}
+
+\input{P_TALS/fct3/polynomfunktionen/Ungleichung_v1}
+
+\section{Umkehrfunktionen}
+\input{P_TALS/fct3/umkehrfunktion/DefinitionsUndWertebereich_v1}
+\end{document}%%

21_22_B/6MT19c_pr4_Polynomfunktionen/clean.sh

+../../clean.sh

21_22_B/6MT19c_pr4_Polynomfunktionen/makeBoth.sh

+../../makeBoth.sh

aufgaben/P_GESO/stoch/kombinatorik/Mississippi_Formel_v1.tex

 
   \leserluft
 
-  Es gibt \LoesungsRaumLang{43\,243\,200} mögliche Zahlen aus den gegebenen Ziffern.
+  Es gibt \LoesungsRaumLang{2\,162\,160} mögliche Zahlen aus den gegebenen Ziffern.
   
-  \platzFuerBerechnungen{4.4}%%
-  \TRAINER{}%%
-  \end{frage} 
+\platzFuerBerechnungen{4.4}%%
+\TRAINER{}%%
+\end{frage}%%

aufgaben/P_GESO/stoch/kombinatorik/Permutation_der_Permutation_v2.tex

 müssen und immer alle Sehenwürdigkeiten im Land «abgehakt» werden,
 bevor die Landesgrenze passiert wird.
 
-Es gibt dafür \LoesungsRaumLang{$5! \cdot{} (3!\cdot{}4!\cdot{}3!\cdot{}4!= 2\,488\,320$)} Varianten.
+Es gibt dafür \LoesungsRaumLang{$5! \cdot{} (3!\cdot{}4!\cdot{}3!\cdot{}4!)= 2\,488\,320$} Varianten.
 \platzFuerBerechnungen{6}%%
 \TRAINER{Für die Lösung ohne 5! gibt es nur einen Punkt.}%%
-\end{frage}
+\end{frage}%%

aufgaben/P_TALS/fct3/polynomfunktionen/AbTextbeschreibung_v1.tex

+\begin{frage}[4]%% Anzahl Punkte für diese Aufgabe
+
+  Eine Polynomfunktion 5. Grades hat eine doppelte Nullstelle bei
+  $x=4$ und eine einfache Nullstelle bei $x=1$. Der
+  $y$-Achsenabschnitt liegt bei 3.5.
+
+  Ferner gehe die Funktion durch die beiden Punkte $P_1=(7|8)$ und $P_2=(3|4)$
+
+  Geben Sie die Funktionsgleichung an (geben Sie jeweils
+  mind 4. sig. Stellen an):
+  
+  $$f(x)=\LoesungsRaum{-0.1718(x-4)(x-4)(x-1)(x-7.1264)(x-0.17868)}$$
+  \platzFuerBerechnungen{8.4}%%
+  \TRAINER{}%%
+\end{frage}

aufgaben/P_TALS/fct3/polynomfunktionen/GeradeAbTextbeschreibung_v1.tex

+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+
+  
+  Berechnen Sie die Funktionsgleichung der Polynomfunktion $p$ mit den
+  folgenden Eigenschaften:
+
+  \begin{itemize}
+  \item Der Grad ist minimal, sodass die folgenden Eigenschaften noch
+    erreichbar sind.
+  \item Der Graph von $p$ ist symmetrisch zur $y$-Achse.
+  \item Die Funktion hat den $y$-Achsenabschnitt 5
+  \item Der Graph der Funktion verläuft durch die Punkte $P=(1|6)$ und
+    $Q=(-5/80)$.
+  \end{itemize} 
+  
+  $$p(x) =\LoesungsRaum{\frac1{12}x^4 + \frac{11}{12}x^2 + 5}$$
+  \platzFuerBerechnungen{8.4}%%
+  \TRAINER{}%%
+\end{frage}

aufgaben/P_TALS/fct3/polynomfunktionen/Grad4_skizzieren_v1.tex

+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+Skizzieren Sie den Graphen der Polynomfunktion $p$ im Bereich $[-6; 6]$:
+
+$p(x) = \frac1{50} (x+5) \cdot{} (x-2)^2 \cdot{} (-x + 3) $
+
+\bbwGraph{-6}{6}{-4}{4}{}
+
+  \platzFuerBerechnungen{4.4}%%
+\TRAINER{}%%
+\end{frage}

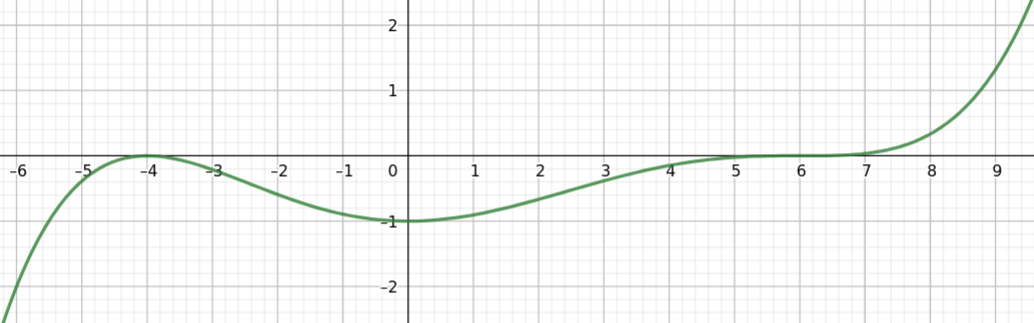
aufgaben/P_TALS/fct3/polynomfunktionen/Grad5_ablesen_v1.tex

+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+
+Die folgende Polynomfunktion berührt die $x$-Achse in $x_1 = -4$ und
+$x_2=6$.
+Geben Sie die Funktionsgleichung an, wenn Sie wissen, dass die
+Funktion den $y$-Achsenabschnitt bei -1 hat:
+  
+\bbwCenterGraphic{14cm}{P_TALS/fct3/polynomfunktionen/img/Grad5_v1.png}
+
+
+
+  $$f(x) =\LoesungsRaum{\frac1{3456}(x+4)(x+4)(x-6)(x-6)(x-6)}$$
+  \platzFuerBerechnungen{16}%%
+\TRAINER{}%%
+\end{frage}

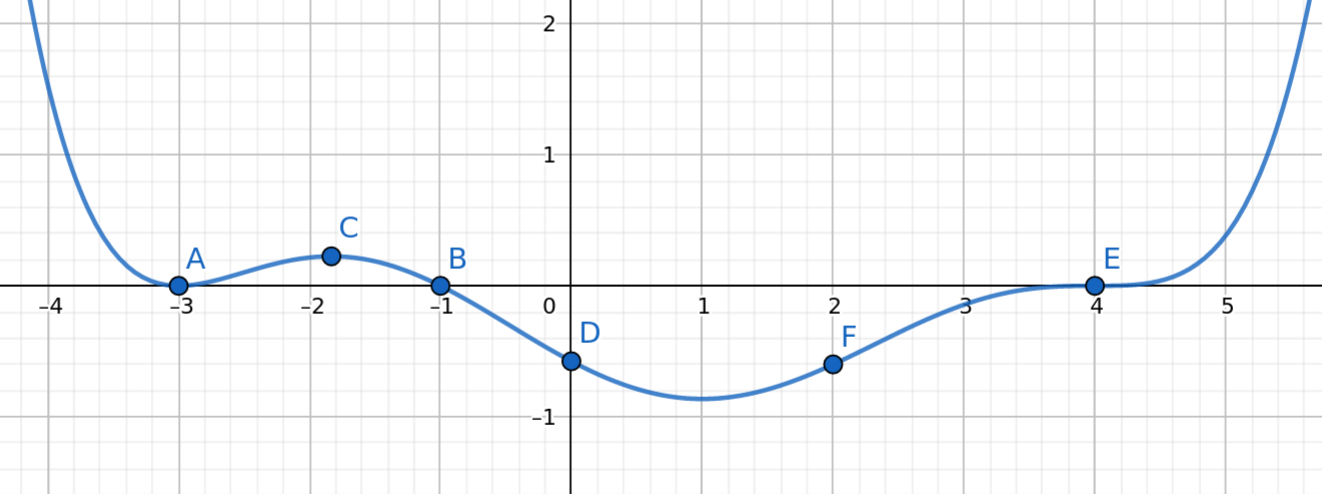
aufgaben/P_TALS/fct3/polynomfunktionen/Punkte_benennen_v1.tex

+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+
+  Benennen Sie alle Punkte des folgenden Graphen. Geben Sie die
+  Antworten möglichst präzise, als nicht nur «Nullstelle» sondern \zB
+  «dreifache Nullstelle»:
+
+  \bbwCenterGraphic{14cm}{P_TALS/fct3/polynomfunktionen/img/CharakteristischePunkteAblesen_v1.png}
+  
+ $$A:=\LoesungsRaum{doppelte Nullstelle}$$
+ $$B:=\LoesungsRaum{einfache Nullstelle}$$
+ $$C:=\LoesungsRaum{lokales Maximum}$$
+ $$D:=\LoesungsRaum{y- Achsenabschnitt}$$
+ $$E:=\LoesungsRaum{dreifache Nullstelle}$$
+ $$F:=\LoesungsRaum{Wendepunkt}$$
+\platzFuerBerechnungen{4.4}%%
+\TRAINER{je 0.5 pkt}%%
+\end{frage}

aufgaben/P_TALS/fct3/polynomfunktionen/Ungleichung_v1.tex

+\begin{frage}[3]%% Anzahl Punkte für diese Aufgabe
+
+  Lösen Sie die folgende Ungleichung graphisch, indem Sie für den Term
+  links bzw. den Term rechts je eine Funktion definieren und diese
+  Funktion qualitativ skizzieren.
+
+  $$1.4(x-3)(x-8) \le -3.8(x-3)(x-5)^2(x-8)$$
+  
+  Sie erhalten einen Punkt für eine brauchbare qualitative Skizze.
+
+  \noTRAINER{\mmPapier{6.4}}
+
+  Geben Sie die Lösungsmenge an:
+
+  $$\lx=\LoesungsRaum{[3; 8]}$$
+  \platzFuerBerechnungen{8.4}%%
+\TRAINER{}%%
+\end{frage}

aufgaben/P_TALS/fct3/umkehrfunktion/DefinitionsUndWertebereich_v1.tex

+\begin{frage}[2]%% Anzahl Punkte für diese Aufgabe
+
+  Gegeben ist die folgende Funktion $f$:
+
+  $$f(x) = 3x-2; \mathbb{D} = [5;7[$$
+
+Geben Sie die Umkehrfunktion $f^{-1}$ mit Definitions- und
+Wertebereich an.
+
+$$f^{-1}(x) = \LoesungsRaumLang{\frac13y+\frac23}$$
+
+$$\mathbb{D}_{f^{-1}} = \LoesungsRaumLang{[13;19[}$$
+$$\mathbb{W}_{f^{-1}} = \LoesungsRaumLang{[5;7[}$$
+
+  \platzFuerBerechnungen{8}%%
+  \TRAINER{}%%
+  \end{frage}